题目内容
一个等腰三角形的顶角是50°,沿一条腰上的高将它对折后得到两个直角三角形,则这两个直角三角形中的两个较大锐角的度数之差是
15
15
度.分析:这个等腰三角形的顶角是50°,它的两个底角相等,是(180°-50°)÷2=65°,沿一条腰上的高将它对折后得到两个直角三角形,其中这两个直角三角形中两个较大的锐角,一个是原等腰三角形的顶角50°,一个底角65°,用65°减去50°就是较大锐角的度数之差.
解答:解:如图,
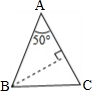
因为AB=AC,∠A=50°
所以∠ABC=∠C=(180°-50°)÷2=65°,
65°-50°=15°;
故答案为:15.

因为AB=AC,∠A=50°
所以∠ABC=∠C=(180°-50°)÷2=65°,
65°-50°=15°;
故答案为:15.
点评:本题考查的知识点有:简单图形的折叠问题、等腰三角形的性质、三角形的内角和等.沿一条腰上的高将它对折后得到两个直角三角形,这两个直角三角形的最大锐角一个是原等腰三角形的顶角,一个是底角.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
一个等腰三角形的顶角是20°,这个三角形一定是( )三角形.
| A、锐角 | B、直角 | C、等边 |
一个等腰三角形的顶角是80°,那么另外两个角分别是( )
| A、50°和50° | B、80°和20° | C、20°和20° |