Question

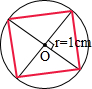
画一个直径是2厘米的圆，再在圆内画一个最大的正方形，并计算出正方形的面积．

Answer 1

分析：因为在圆中所画最大正方形的对角线就等于圆的直径，圆的直径已知，从而可以求出正方形的对角线的长度，也就能求出正方形的面积．

解答：解：以点O为圆心，以2÷2=1厘米为半径画圆，
再画出这个圆的两条互相垂直的直径，
依次连接两条直径的四个端点，所形成的四边形，就是所要求画的正方形，
其面积为：2×（2÷2）÷2×2，
=2×1，
=2（平方厘米）；
．
答：这个正方形的面积是2平方厘米．

点评：解答此题的关键是明白，圆中所画最大正方形的对角线就等于圆的直径．