题目内容
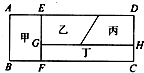 如图,一块长方形的布料ABCD,被剪成大小相等的甲、乙、丙、丁四块,其中甲块布料的长与宽的比为a:b=3:2,那么丁块布料的长与宽的比是
如图,一块长方形的布料ABCD,被剪成大小相等的甲、乙、丙、丁四块,其中甲块布料的长与宽的比为a:b=3:2,那么丁块布料的长与宽的比是6:1
6:1
.分析:由题意可知:甲、乙、丙、丁的面积相等,则可以设甲布料长3x,宽为2x,则每一块的面积是6x2,大长方形的面积就是24x2,进而可以用x分别表示出大长方形的长和宽,再据丁的长和宽与甲的长和宽关系,因此可以用x表示出乙的长和宽,于是可以求出乙的长和宽的比.
解答:解:由题意得四块布料的面积相等,
设甲布料长3x,宽2x,面积为6x2,
所以总面积是24x2,
总面积=总长×总宽=总长×3x
所以总长=8x,
丁长+甲宽=总长,
所以丁长=6x,
而丁的面积=6x2,
丁宽=丁面积÷丁长=x,
所以丁块布料的长与宽的比是6:1;
答:丁块布料的长与宽的比是6:1.
故答案为:6:1.
设甲布料长3x,宽2x,面积为6x2,
所以总面积是24x2,
总面积=总长×总宽=总长×3x
所以总长=8x,
丁长+甲宽=总长,
所以丁长=6x,
而丁的面积=6x2,
丁宽=丁面积÷丁长=x,
所以丁块布料的长与宽的比是6:1;
答:丁块布料的长与宽的比是6:1.
故答案为:6:1.
点评:解答此题的关键是:设出甲的长和宽,进而依据面积的关系,求出丁的长和宽的比.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
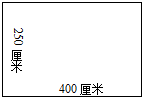 妈妈买了一块长方形的花布(如图)
妈妈买了一块长方形的花布(如图) 妈妈买了一块长方形的花布(如图)
妈妈买了一块长方形的花布(如图)