题目内容
14.“60个零件中有一个次品(次品轻一些),用天平称,至少称几次就一定能找出次品来?”使用正确的方法称两次后,可以将次品的范围确定在6或7个零件中.分析 ①第一步:从60个零件中任取30个平均分成两份,每份15个,分别放在天平秤两端,若天平秤平衡,则不合格的零件在未取的30个零件中,再按照下面的方法继续直到找出不合格零件为止.若不平衡,第二步:从比较轻的15个零件中,任取10个平均分成两份,每份5个,分别放在天平秤两端,若天平秤平衡,则不合格的零件在未取得15个零件中,再按下面的方法继续直到找出不合格零件为止.若天平秤不平衡,第三步:从较轻的5个零件中任取4个平均分成两份,每份2个,若天平秤平衡,则未取的零件即为不合格零件.若不平衡,第四步:把两个比较轻的零件分别放在天平秤两端,较轻的即为不合格零件.
②首先把60个零件平均分成3份,每份是20个;
天平两边均放20个,无论平不平衡,次品都在20个中;
再把20个分为7个,7个,6个;天平一边放7个,平衡次品在6个中,不平衡,次品在7个中
所以使用正确的方法称两次后,可以将次品的范围确定在6或7个零件中.
据此即可解答.
解答 解:①依据分析可得:质检员用天平至少称4次,保证能找到这个不合格的零件.
图示为: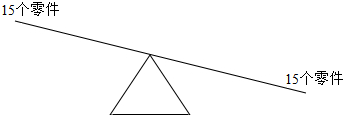
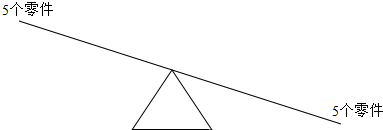
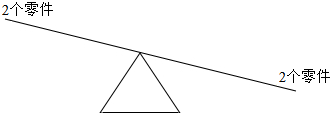
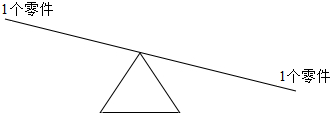
②首先把60个零件平均分成3份,每份是20个;
天平两边均放20个,无论平不平衡,次品都在20个中;
再把20个分为7个,7个,6个;天平一边放7个,平衡次品在6个中,不平衡,次品在7个中
所以使用正确的方法称两次后,可以将次品的范围确定在6或7个零件中.
答:至少称4次就一定能找出次品来,使用正确的方法称两次后,可以将次品的范围确定在6或7个零件中.
故答案为:6或7.
点评 本题主要考查学生根据天平秤平衡原理解决问题的能力.

练习册系列答案
相关题目
17.将63.5的小数点向左移动两位,这个数就( )
| A. | 缩小到原数的$\frac{1}{2}$ | B. | 扩大到原数的100倍 | ||
| C. | 缩小到原数的$\frac{1}{100}$ |

 阴影部分面积与长方形面积的比是2:5,与平行四边形的面积的比是1:4.那么长方形面积和平行四边形面积的比是几比几?
阴影部分面积与长方形面积的比是2:5,与平行四边形的面积的比是1:4.那么长方形面积和平行四边形面积的比是几比几?