题目内容
下面是由边长为a的小正方形和边长为b的大正方形组成的图形,用字母表示涂色部分的面积.
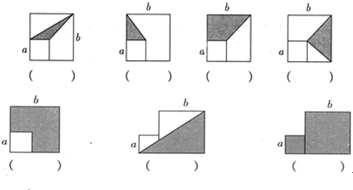

分析:(1)(2)观察图形可知,阴影部分的三角形的底是a,高是b-a,利用三角形的面积公式即可解答;
(3)观察图形可知,上底是a、下底是b、高是b-a,据此利用梯形的面积公式计算即可;
(4)底是b,高是b-a,再利用三角形的面积公式计算即可解答;
(5)阴影部分的面积等于边长是b和边长是a的正方形的面积之差;
(6)阴影部分是底a+b、高是b的三角形的面积,据此利用三角形的面积公式计算即可解答;
(7)阴影部分的面积等于这两个正方形的面积之和.
(3)观察图形可知,上底是a、下底是b、高是b-a,据此利用梯形的面积公式计算即可;
(4)底是b,高是b-a,再利用三角形的面积公式计算即可解答;
(5)阴影部分的面积等于边长是b和边长是a的正方形的面积之差;
(6)阴影部分是底a+b、高是b的三角形的面积,据此利用三角形的面积公式计算即可解答;
(7)阴影部分的面积等于这两个正方形的面积之和.
解答:解:根据题干分析可得:
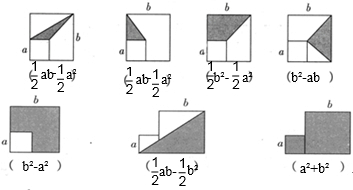
(1)(2)a×(b-a)÷2=
ab-
a2;
(3)(a+b)×(b-a)÷2=
(a+b)(b-a)=
b2-
a2;
(4)b(b-a)=b2-ab;
(5)b2-a2;
(6)(a+b)×b÷2=
ab+
b2;
(7)a2+b2;
故答案为:
(1)(2)a×(b-a)÷2=
| 1 |
| 2 |
| 1 |
| 2 |
(3)(a+b)×(b-a)÷2=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(4)b(b-a)=b2-ab;
(5)b2-a2;
(6)(a+b)×b÷2=
| 1 |
| 2 |
| 1 |
| 2 |
(7)a2+b2;
故答案为:

点评:此题主要考查组合图形的面积的计算方法,关键是明确这个图形的面积包括哪几个部分.

练习册系列答案
相关题目





