题目内容
A、B都是自然数,A>B,A+B=64,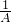 +
+ =
= .则A-B=________.
.则A-B=________.
32
分析: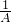 +
+ =
= ,可知
,可知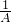
 ,
, <
< ,即A>12,B>12,又因A>B,可知B是一个大于13且小于32的自然数,然后分情况讨论,可分别求出A、B的值,据此解答.
,即A>12,B>12,又因A>B,可知B是一个大于13且小于32的自然数,然后分情况讨论,可分别求出A、B的值,据此解答.
解答:根据以上分析可,13<B<32,
当B=13,A=51时,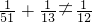 ,
,
当B=14.A=50时, ≠
≠ ,
,
当B=15.A=49时, ≠
≠ ,
,
当B=16.A=48时, =
= ,
,
当B=17.A=47时,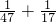 ≠
≠ ,
,
当B=18.A=46时, ≠
≠ ,
,
当B=19.A=45时,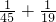 ≠
≠ ,
,
当B=20.A=44时,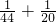 ≠
≠ ,
,
当B=21.A=43时,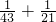 ≠
≠ ,
,
当B=22.A=42时, ≠
≠ ,
,
当B=23.A=41时,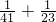 ≠
≠ ,
,
当B=24.A=40时, ≠
≠ ,
,
当B=25.A=39时,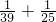 ≠
≠ ,
,
当B=26.A=38时,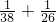 ≠
≠ ,
,
当B=27.A=37时, ≠
≠ ,
,
当B=28.A=36时, ≠
≠ ,
,
当B=29.A=35时,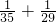 ≠
≠ ,
,
当B=30.A=34时, ≠
≠ ,
,
当B=31.A=33时,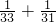 ≠
≠ ,
,
只有当B=16,A=48时,才满足A、B都是自然数,A>B,A+B=64,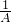 +
+ =
= .
.
48-16=32.
故答案为:32.
点评:本题的关键是根据分数加法和的变化规律,分情况讨论B的情况,再进行解答.
分析:
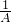 +
+ =
= ,可知
,可知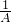
 ,
, <
< ,即A>12,B>12,又因A>B,可知B是一个大于13且小于32的自然数,然后分情况讨论,可分别求出A、B的值,据此解答.
,即A>12,B>12,又因A>B,可知B是一个大于13且小于32的自然数,然后分情况讨论,可分别求出A、B的值,据此解答.解答:根据以上分析可,13<B<32,
当B=13,A=51时,
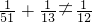 ,
,当B=14.A=50时,
 ≠
≠ ,
,当B=15.A=49时,
 ≠
≠ ,
,当B=16.A=48时,
 =
= ,
,当B=17.A=47时,
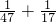 ≠
≠ ,
,当B=18.A=46时,
 ≠
≠ ,
,当B=19.A=45时,
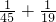 ≠
≠ ,
,当B=20.A=44时,
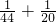 ≠
≠ ,
,当B=21.A=43时,
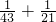 ≠
≠ ,
,当B=22.A=42时,
 ≠
≠ ,
,当B=23.A=41时,
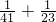 ≠
≠ ,
,当B=24.A=40时,
 ≠
≠ ,
,当B=25.A=39时,
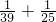 ≠
≠ ,
,当B=26.A=38时,
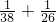 ≠
≠ ,
,当B=27.A=37时,
 ≠
≠ ,
,当B=28.A=36时,
 ≠
≠ ,
,当B=29.A=35时,
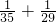 ≠
≠ ,
,当B=30.A=34时,
 ≠
≠ ,
,当B=31.A=33时,
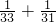 ≠
≠ ,
,只有当B=16,A=48时,才满足A、B都是自然数,A>B,A+B=64,
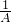 +
+ =
= .
.48-16=32.
故答案为:32.
点评:本题的关键是根据分数加法和的变化规律,分情况讨论B的情况,再进行解答.

练习册系列答案
相关题目
a、b都是自然数,a÷□=b…38,除数最小是( )
| A、39 | B、38 | C、37 |