题目内容
 如图所示,阴影正方形的面积是2平方厘米,以这个正方形的对角线为边作第二个正方形;再以第二个正方形的对角线为边作第三个正方形.照此法依次作下去.问:
如图所示,阴影正方形的面积是2平方厘米,以这个正方形的对角线为边作第二个正方形;再以第二个正方形的对角线为边作第三个正方形.照此法依次作下去.问:
(1)第100个正方形的面积是多少平方厘米?
(2)这100个正方形的面积之和是多少平方厘米?
(3)这100个正方形实际覆盖的面积是多少平方厘米?
解:(1)由题意得:第二个正方形的面积是2×2=4=22,
第三个正方形的面积是4×2=8=23,
第四个正方形的面积是8×2=16=24,
…
依此类推,则Sn=2n.
所以第100个正方形的面积是:2100平方厘米.
答:第100个正方形的面积是2100平方厘米;
(2)这100个正方形的面积之和是:21+22+23+…+2100=2101-2(平方厘米);
答:这100个正方形的面积之和是2101-2平方厘米.
(3)(2101-2)× =2100-1(平方厘米).
=2100-1(平方厘米).
答:这100个正方形实际覆盖的面积是2100-1平方厘米.
分析:(1)根据已知可发现第n个正方形面积是第(n-1)个面积的2倍,所以第100个正方形面积是2100,据此解答即可.
(2)将100个正方形面积相加即可
(3)由图意得出这100个正方形实际覆盖的面积是这100个正方形面积和的一半.
点评:主要考查了学生通过特例分析从而归纳总结出一般结论的能力.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解.
第三个正方形的面积是4×2=8=23,
第四个正方形的面积是8×2=16=24,
…
依此类推,则Sn=2n.
所以第100个正方形的面积是:2100平方厘米.
答:第100个正方形的面积是2100平方厘米;
(2)这100个正方形的面积之和是:21+22+23+…+2100=2101-2(平方厘米);
答:这100个正方形的面积之和是2101-2平方厘米.
(3)(2101-2)×
 =2100-1(平方厘米).
=2100-1(平方厘米).答:这100个正方形实际覆盖的面积是2100-1平方厘米.
分析:(1)根据已知可发现第n个正方形面积是第(n-1)个面积的2倍,所以第100个正方形面积是2100,据此解答即可.
(2)将100个正方形面积相加即可
(3)由图意得出这100个正方形实际覆盖的面积是这100个正方形面积和的一半.
点评:主要考查了学生通过特例分析从而归纳总结出一般结论的能力.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
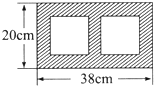 一种水泥空心砖的横截面如图所示(阴影部分),它的空心部分是两个边长16cm的正方形,请你求出空心砖的横截面积.
一种水泥空心砖的横截面如图所示(阴影部分),它的空心部分是两个边长16cm的正方形,请你求出空心砖的横截面积.
 如图所示,以正方形的边为直径在正方形内作半圆,则圆中阴影部分面积与正方形面积比为( )
如图所示,以正方形的边为直径在正方形内作半圆,则圆中阴影部分面积与正方形面积比为( )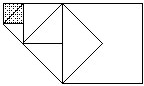 如图所示,阴影正方形的面积是2平方厘米,以这个正方形的对角线为边作第二个正方形;再以第二个正方形的对角线为边作第三个正方形.照此法依次作下去.问:
如图所示,阴影正方形的面积是2平方厘米,以这个正方形的对角线为边作第二个正方形;再以第二个正方形的对角线为边作第三个正方形.照此法依次作下去.问: