题目内容
长方形的宽减少 ,要使面积不变,长必须增加________%.
,要使面积不变,长必须增加________%.
50
分析:设长方形原来的长和宽分别是2和1;根据“长方形的面积=长×宽”计算出原来的长方形的面积;然后根据一个数乘分数的意义,分别计算出后来长方形的宽,再用面积除以宽,求出后来长方形的长,进而求出增加的长方形的长,再用增加的长度除以原来长方形的长即可.
解答:设长方形原来的长和宽分别是2和1,那么:
面积是:2×1=2;
后来的宽是:1×(1- )=
)= ;
;
后来的长是:2÷ =3;
=3;
长增加的百分数是:
(3-2)÷2,
=1÷2,
=50%;
答:长必须增加50%.
故答案为:50.
点评:解答此题的关键是先设出原来长方形的长和宽,进而根据长方形的面积计算方法求出原来的长方形的面积;再计算出后来长方形的宽,根据面积相等求出后来的长,再根据求一个数是另一个数百分之几的方法求解.
分析:设长方形原来的长和宽分别是2和1;根据“长方形的面积=长×宽”计算出原来的长方形的面积;然后根据一个数乘分数的意义,分别计算出后来长方形的宽,再用面积除以宽,求出后来长方形的长,进而求出增加的长方形的长,再用增加的长度除以原来长方形的长即可.
解答:设长方形原来的长和宽分别是2和1,那么:
面积是:2×1=2;
后来的宽是:1×(1-
 )=
)= ;
;后来的长是:2÷
 =3;
=3;长增加的百分数是:
(3-2)÷2,
=1÷2,
=50%;
答:长必须增加50%.
故答案为:50.
点评:解答此题的关键是先设出原来长方形的长和宽,进而根据长方形的面积计算方法求出原来的长方形的面积;再计算出后来长方形的宽,根据面积相等求出后来的长,再根据求一个数是另一个数百分之几的方法求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
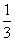 ,要使面积不变,长必须增加( )%。
,要使面积不变,长必须增加( )%。