题目内容
一块长方形的布,长120cm,宽90cm,把它做成同样大小的正方形手绢,且没有剩余,手绢的边长最长是多少cm?可做成多少块这样的手绢?
解:120=2×2×2×3×5,90=2×3×3×5,
所以120和90的最大公因数是:2×3×5=30,即正方形手绢的边长是30厘米;
(120÷30)×(90÷30),
=4×3,
=12(块);
答:手绢的边长最长是30cm,可做成12块这样的手绢.
分析:由做成同样大小的正方形手绢,且没有剩余,可知:正方形手绢的边长是120和90的公因数,要求手绢的边长最长是多少cm,就是正方形手绢的边长是120和90的最大公因数,用120和90分别除以它们的最大公因数,然后把它们的商乘起来,得到的积就是可做成多少块这样的手绢.
点评:解答本题关键是理解:做成同样大小的正方形手绢,且没有剩余,就是正方形手绢的边长是120和90的公因数.
所以120和90的最大公因数是:2×3×5=30,即正方形手绢的边长是30厘米;
(120÷30)×(90÷30),
=4×3,
=12(块);
答:手绢的边长最长是30cm,可做成12块这样的手绢.
分析:由做成同样大小的正方形手绢,且没有剩余,可知:正方形手绢的边长是120和90的公因数,要求手绢的边长最长是多少cm,就是正方形手绢的边长是120和90的最大公因数,用120和90分别除以它们的最大公因数,然后把它们的商乘起来,得到的积就是可做成多少块这样的手绢.
点评:解答本题关键是理解:做成同样大小的正方形手绢,且没有剩余,就是正方形手绢的边长是120和90的公因数.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
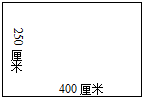 妈妈买了一块长方形的花布(如图)
妈妈买了一块长方形的花布(如图) 妈妈买了一块长方形的花布(如图)
妈妈买了一块长方形的花布(如图)