题目内容
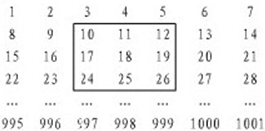
将1到1001的各数如图格式排列,我们可以用一对数来表示每个数的位置,如16在第三行第二列,可表示为(3,2),用一个正方形框出9个数(如图,有三列三行),要使框出的9个数之和等于2007,那么,这个正方形里的最大数的位置是________.
(33,7)
分析:从数表中可以发现:用正方形框出9个数中间的数是9的倍数,由此可求出框出的9个数之和等于2007的中间数是2007÷9=223,再由用一个正方形框出9个数的特点即每行中相邻的两个数差1,每列中相邻的两个数差7,由此求出223下面的数是223+7=230,则最大的数是231;最后再根据1到1001的数排列特点每行7个数,乘S型排列并且第七列的数是7的倍数即可解答.
解答:2007÷9+7+1
=223+7+1
=231;
231÷7=33,
所以这个正方形里的最大数的位置是(33,7)
故答案为:33,7.
点评:考查了数表中的规律,解答本题的关键发现中间数是9的倍数的规律,以及1到1001的数排列特点每行7个数,乘S型排列并且第七列的数是7的倍数.
分析:从数表中可以发现:用正方形框出9个数中间的数是9的倍数,由此可求出框出的9个数之和等于2007的中间数是2007÷9=223,再由用一个正方形框出9个数的特点即每行中相邻的两个数差1,每列中相邻的两个数差7,由此求出223下面的数是223+7=230,则最大的数是231;最后再根据1到1001的数排列特点每行7个数,乘S型排列并且第七列的数是7的倍数即可解答.
解答:2007÷9+7+1
=223+7+1
=231;
231÷7=33,
所以这个正方形里的最大数的位置是(33,7)
故答案为:33,7.
点评:考查了数表中的规律,解答本题的关键发现中间数是9的倍数的规律,以及1到1001的数排列特点每行7个数,乘S型排列并且第七列的数是7的倍数.

练习册系列答案
相关题目
 将1到1001的各数如图格式排列,我们可以用一对数来表示每个数的位置,如16在第三行第二列,可表示为(3,2),用一个正方形框出9个数(如图,有三列三行),要使框出的9个数之和等于2007,那么,这个正方形里的最大数的位置是
将1到1001的各数如图格式排列,我们可以用一对数来表示每个数的位置,如16在第三行第二列,可表示为(3,2),用一个正方形框出9个数(如图,有三列三行),要使框出的9个数之和等于2007,那么,这个正方形里的最大数的位置是