题目内容
18．
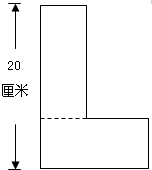如图，周长为64厘米的“L”形纸片可沿虚线分成两个完全相同的长方形，如果最长的边长是20厘米，那么该“L”形纸片的面积是多少平方厘米？
分析 
观察上图，把EF移到和CG一条边，FG移到和AE一条边，（AB+BC）×2=64，AB+BC=32，BC=32-20=12，
因为两个小长方形相同，所以AH=BC=12，HB=AB-AH=20-12=8，所以小长方形的长是12，宽是8，利用长方形的面积公式=长×宽求出一个小长方形的面积，然后再乘2就是L形纸片的面积．
解答 解：64÷2-20
=32-20
=12（厘米）
设小长方形的宽是x厘米，那么小长方形的长就是20-x厘米，也就是12厘米，
所以：20-x=12
x=20-12
x=8
12×8×2=192（平方厘米）
答：该“L”形纸片的面积是192平方厘米．
点评 这道题要先求出纸片的下面的边的长度，也就是小长方形的长，再求出小长方形的宽，然后求出一个小长方形的面积，再乘2即可得到所求．
练习册系列答案
相关题目
8．直接写出得数：
| $\frac{1}{2}$-$\frac{1}{5}$= | 2-$\frac{4}{5}$= | $\frac{9}{7}$-$\frac{1}{2}$= | $\frac{1}{4}$÷$\frac{1}{2}$= | $\frac{1}{5}$÷$\frac{5}{4}$= |
| $\frac{1}{4}$+$\frac{1}{3}$= | $\frac{8}{7}$×$\frac{7}{16}$= | $\frac{5}{8}$÷$\frac{5}{8}$= | $\frac{5}{54}$×9= | $\frac{7}{9}$÷$\frac{7}{9}$×$\frac{7}{9}$÷$\frac{7}{9}$= |
6．“保护环境，人人有责！”学校组织同学们成立了环保小组．其中一名组员小华利用假期收集费电池，第一天收集了1号电池4节，5号电池5节，总重量为460克；第二天收集1号电池8节，5号电池6节，总重量为840克．
（1）1号电池和5号电池每节分别重多少克？
（2）这个环保小组又全体出动，连续收集五天，这五天每天收集废电池的数量如表：
问：平均每天收集多少节1号电池、多少节5号电池？平均每天收集废电池的总重量是多少克？
（1）1号电池和5号电池每节分别重多少克？
（2）这个环保小组又全体出动，连续收集五天，这五天每天收集废电池的数量如表：
| 第一天 | 第二天 | 第三天 | 第四天 | 第五天 | |
| 1号电池（单位：节） | 29 | 30 | 32 | 28 | 31 |
| 5号电池（单位：节） | 51 | 53 | 47 | 49 | 50 |
