题目内容
 已知图中大正方形的边长是12厘米,小正方形的边长是8厘米,阴影部份的面积是
已知图中大正方形的边长是12厘米,小正方形的边长是8厘米,阴影部份的面积是32
32
平方厘米.分析:如图所示,连接BC,则三角形ABC和三角形CEB等底等高,则二者的面积相等,它们分别去掉公共部分三角形CFB,剩余部分的面积仍然相等,即三角形CEF的面积和三角形ABF的面积相等,于是阴影部分就转化成了小正方形的面积的一半,问题得解.
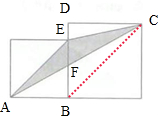

解答:解:连接BC,
则S△ABC=S△CEB,
于是S△ABC-S△CFB=S△CEB-S△CFB,
即S△ABF=S△CEF,
所以阴影部分的面积=
a2,
=
×82,
=
×64,
=32(平方厘米);
答:阴影部分的面积是32平方厘米.
故答案为:32.
则S△ABC=S△CEB,
于是S△ABC-S△CFB=S△CEB-S△CFB,
即S△ABF=S△CEF,
所以阴影部分的面积=
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=32(平方厘米);
答:阴影部分的面积是32平方厘米.
故答案为:32.
点评:解答此题的关键是作出辅助线,将阴影部分的面积转化成小正方形的面积的一半,问题即可得解.

练习册系列答案
相关题目
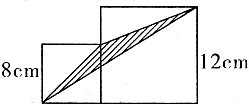 已知图中大正方形边长是12cm,小正方形边长是8cm,求图中阴影部分的面积.
已知图中大正方形边长是12cm,小正方形边长是8cm,求图中阴影部分的面积.
 已知图中大正方形的边长是12厘米,小正方形的边长是8厘米,阴影部份的面积是________平方厘米.
已知图中大正方形的边长是12厘米,小正方形的边长是8厘米,阴影部份的面积是________平方厘米.