题目内容
 如图,已知两同心圆(圆心相同,半径不相等的两个圆),大圆半径为3厘米,小圆半径为1厘米,则阴影部分的面积为
如图,已知两同心圆(圆心相同,半径不相等的两个圆),大圆半径为3厘米,小圆半径为1厘米,则阴影部分的面积为12.56
12.56
平方厘米(精确到0.01).分析:如图所示,根据圆的对称性,大圆与小圆之间的部分全等,故阴影部分的面积是两圆面积差的一半.
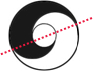

解答:解:观察图形,发现:阴影部分的面积是两圆面积差的一半,
即S阴影=
(S大圆-S小圆),
=
π(32-12),
=4π,
=4×3.14,
=12.56(平方厘米);
答:阴影部分的面积是12.56平方厘米.
故答案为:12.56.
即S阴影=
| 1 |
| 2 |
=
| 1 |
| 2 |
=4π,
=4×3.14,
=12.56(平方厘米);
答:阴影部分的面积是12.56平方厘米.
故答案为:12.56.
点评:本题考查圆环面积的计算.求出圆环的面积,即大圆面积减去小圆的面积,而阴影部分面积等于圆环面积的一半.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知两同心圆(圆心相同,半径不相等的两个圆),大圆半径为3厘米,小圆半径为1厘米,则阴影部分的面积为________平方厘米(精确到0.01).
如图,已知两同心圆(圆心相同,半径不相等的两个圆),大圆半径为3厘米,小圆半径为1厘米,则阴影部分的面积为________平方厘米(精确到0.01).