题目内容
 如图所示的8行8列的数阵中,其中的全、国、春、蕾、杯、小、学、生、思、维、邀、请、赛、试、题表示从小到大的15个连续的自然数,把这个数阵分成四个4行4列的数阵(如下右图),已知右下部分中所有数的和是560.请问:这个8行8列的数阵中所有数的和是多少?
如图所示的8行8列的数阵中,其中的全、国、春、蕾、杯、小、学、生、思、维、邀、请、赛、试、题表示从小到大的15个连续的自然数,把这个数阵分成四个4行4列的数阵(如下右图),已知右下部分中所有数的和是560.请问:这个8行8列的数阵中所有数的和是多少?分析:可设思为x,用x表示出维、邀、请、赛、试、题,根据右下部分中所有数的和是560可得关于x的方程,求得x的值,从而得到全、国、春、蕾、杯、小、学、生、思、维、邀、请、赛、试、题表示的数,依此即可得到这个8行8列的数阵中所有数的和.
解答:解:设思为x,则维为x+1、邀为x+2、请为x+3、赛为x+4、试为x+5、题为x+6,则
x+2(x+1)+3(x+2)+4(x+3)+3(x+4)+2(x+5)+x+6=560,
16x+48=560,
16x=512,
x=32.
则全=24、国=25、春=26、蕾=27、杯=28、小=29、学=30、生=31、思=32、维=33、邀=34、请=35、赛=36、试=37、题=38,
则这个8行8列的数阵中所有数的和是
24+25×2+26×3+27×4+28×5+29×6+30×7+31×8+32×7+33×6+34×5+35×4+36×3+37×2+38,
=24+50+78+108+140+174+210+248+224+198+170+140+108+74+38,
=1984.
答:这个8行8列的数阵中所有数的和是1984.
x+2(x+1)+3(x+2)+4(x+3)+3(x+4)+2(x+5)+x+6=560,
16x+48=560,
16x=512,
x=32.
则全=24、国=25、春=26、蕾=27、杯=28、小=29、学=30、生=31、思=32、维=33、邀=34、请=35、赛=36、试=37、题=38,
则这个8行8列的数阵中所有数的和是
24+25×2+26×3+27×4+28×5+29×6+30×7+31×8+32×7+33×6+34×5+35×4+36×3+37×2+38,
=24+50+78+108+140+174+210+248+224+198+170+140+108+74+38,
=1984.
答:这个8行8列的数阵中所有数的和是1984.
点评:考查了数阵图中找规律的问题,本题根据是设思为x,由等量关系:右下部分中所有数的和是560,列出方程求得x的值,有一定的难度,计算量也较大.

练习册系列答案
相关题目
 在如图所示的8行8列的方格表中,每个空格分别填上1,2,3这三个数字中的任一个,使得每行、每列及两条对角线上的各个数字的和互不相等,能不能做到?
在如图所示的8行8列的方格表中,每个空格分别填上1,2,3这三个数字中的任一个,使得每行、每列及两条对角线上的各个数字的和互不相等,能不能做到?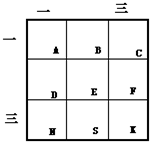 玛丽和老师做游戏,两人轮流在如图所示的正方形网格中任意一格内填数,所填的数只能是1、3、4、5、6、7、8、9、10这9个数.每个数只能用一次.全部填完后,一、三两行数的和为玛丽的得分,一、三两列数的和为老师的得分,得分高的人获胜.玛丽首先填数,要想一定取胜的话,最初要在哪一方格中填哪个数?请说明理由.
玛丽和老师做游戏,两人轮流在如图所示的正方形网格中任意一格内填数,所填的数只能是1、3、4、5、6、7、8、9、10这9个数.每个数只能用一次.全部填完后,一、三两行数的和为玛丽的得分,一、三两列数的和为老师的得分,得分高的人获胜.玛丽首先填数,要想一定取胜的话,最初要在哪一方格中填哪个数?请说明理由.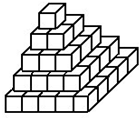 有55个棱长为1分米的正方体木块连体,在地面上摆成如图所示的形式,要在表面涂刷油漆,如果与地面接触的面不涂油漆,干后将小木块分开,则涂油漆的表面积与未涂油漆表面积的比是
有55个棱长为1分米的正方体木块连体,在地面上摆成如图所示的形式,要在表面涂刷油漆,如果与地面接触的面不涂油漆,干后将小木块分开,则涂油漆的表面积与未涂油漆表面积的比是 在如图所示的8行8列的方格表中,每个空格分别填上1,2,3这三个数字中的任一个,使得每行、每列及两条对角线上的各个数字的和互不相等,能不能做到?
在如图所示的8行8列的方格表中,每个空格分别填上1,2,3这三个数字中的任一个,使得每行、每列及两条对角线上的各个数字的和互不相等,能不能做到?