题目内容
用6个长、宽、高分别为1、2、3的小长方体组成一个大长方体,则这个大长方体的面积最小为________.
66
分析:要使这个大长方体的表面积最小,则可以把小长方体的最大的面粘合在一起,粘合在一起的面越多,所得到的长方体的表面积最小,如图:所以把6个长方体分成2组,每3个长方体
都把最大的3×2面相连,再把这两组图形拼成的最大的3×3面连接起来,正好组成了一个长宽高分别为3、4、3的长方体,由此利用长方体的表面积公式计算即可.
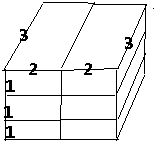
解答:根据题干将这6个长方体按照上述方法拼组成大长方体,
则表面积是:(3×4+3×3+4×3)×2,
=(12+9+12)×2,
=33×2,
=66;
答:这个大长方体的面积最小为66.
故答案为:66.
点评:解答此类问题的关键是:把最大面相连接进行拼组,则拼组后的长方体的表面积最小.
分析:要使这个大长方体的表面积最小,则可以把小长方体的最大的面粘合在一起,粘合在一起的面越多,所得到的长方体的表面积最小,如图:所以把6个长方体分成2组,每3个长方体
都把最大的3×2面相连,再把这两组图形拼成的最大的3×3面连接起来,正好组成了一个长宽高分别为3、4、3的长方体,由此利用长方体的表面积公式计算即可.

解答:根据题干将这6个长方体按照上述方法拼组成大长方体,
则表面积是:(3×4+3×3+4×3)×2,
=(12+9+12)×2,
=33×2,
=66;
答:这个大长方体的面积最小为66.
故答案为:66.
点评:解答此类问题的关键是:把最大面相连接进行拼组,则拼组后的长方体的表面积最小.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目