题目内容
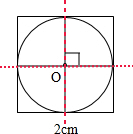
 在下面边长2厘米的正方形中画出一个最大的圆,并画出圆的两条对称轴,使这两条对称轴互相垂直.并计算这个圆的周长和剩下的面积.
在下面边长2厘米的正方形中画出一个最大的圆,并画出圆的两条对称轴,使这两条对称轴互相垂直.并计算这个圆的周长和剩下的面积.分析:(1)以正方形的两组对边中线的交点为圆心,正方形的边长的一半为半径,所画出的圆就是在正方形中最大的圆,正方形的两组对边的中线所在的直线就是圆的互相垂直的两条对称轴.
(2)因为圆的直径等于正方形的边长,利用圆的周长C=πd,即可求出这个圆的周长;剩下的面积=正方形的面积-圆的面积,分别利用正方形和圆的面积公式即可求解.
(2)因为圆的直径等于正方形的边长,利用圆的周长C=πd,即可求出这个圆的周长;剩下的面积=正方形的面积-圆的面积,分别利用正方形和圆的面积公式即可求解.
解答:解:(1)如图所示,以正方形的两组对边中线的交点O为圆心,2÷2=1厘米为半径,
所画出的圆就是在正方形中最大的圆.
(2)圆的周长:
3.14×2=6.28(厘米);
剩下的面积:
2×2-3.14×(
)2,
=4-3.14,
=0.86(平方厘米);
答:这个圆的周长是6.28厘米,剩下得面积是0.86平方厘米.
所画出的圆就是在正方形中最大的圆.

(2)圆的周长:
3.14×2=6.28(厘米);
剩下的面积:
2×2-3.14×(
| 2 |
| 2 |
=4-3.14,
=0.86(平方厘米);
答:这个圆的周长是6.28厘米,剩下得面积是0.86平方厘米.
点评:(1)确定好圆心的位置和半径的长度,即可画出符合要求的圆.
(2)此题主要考查圆的周长和正方形以及圆的面积的计算方法.
(2)此题主要考查圆的周长和正方形以及圆的面积的计算方法.

练习册系列答案
相关题目
 (1)画一个边长2厘米的正方形
(1)画一个边长2厘米的正方形 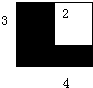 在一张长4厘米,宽3厘米的长方形中,剪去一个边长2厘米的正方形.
在一张长4厘米,宽3厘米的长方形中,剪去一个边长2厘米的正方形.
 在下面边长2厘米的正方形中画出一个最大的圆,并画出圆的两条对称轴,使这两条对称轴互相垂直.并计算这个圆的周长和剩下的面积.
在下面边长2厘米的正方形中画出一个最大的圆,并画出圆的两条对称轴,使这两条对称轴互相垂直.并计算这个圆的周长和剩下的面积.