题目内容
9．如图，在△ABC中，AB＞AC，AD为∠A的平分线，求证：AB-AC＞BD-CD．
分析 已知AB＞AC，在AB上截取AE等于AC，首先证明三角形ADE和三角形ACD全等，由此得出DE=DC，进而得出AB-AC＞BD-CD．
解答 解：如图：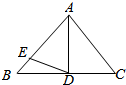
证明：在AB上截取AE=AC．连接DE，
因为AD是三角形ABC的角平分线，所以△AED≌△ACD（SAS），
所以DE=DC，在△BDE中，BE＞BD-DE=BD-DC，即AB-AC＞BD-DC．
点评 此题解答根据是作辅助线DE，通过证明三角形AED和三角形ACD全等，进而得出结论．
练习册系列答案
春雨教育同步作文系列答案
相关题目
20．口算．
| 478-70= | 20×50= | 80×12= | 16×40= | 10×30= |
| 15×3= | 30×25= | 19×20= | 25×8= | 20×60= |
| 20+42= | 0×687= | 40×7= | 35×2= | 9×30= |
