题目内容
在正方形里面画一个最大的圆,圆面积是正方形面积的
,在圆里面画一个最大的正方形,正方形面积是圆面积的
.(结果中的π保留,不必取近似值计算)
| π |
| 4 |
| π |
| 4 |
| 2 |
| π |
| 2 |
| π |
分析:在正方形中画的最大圆的直径就等于正方形的边长,分别利用圆和正方形的面积公式表示出它们的面积,即可求得圆面积是正方形面积的几分之几;
在圆中画的最大正方形的对角线就是圆的直径,从而可以分别利用圆和正方形的面积公式表示出它们的面积,即可求得正方形面积是圆面积的几分之几;
在圆中画的最大正方形的对角线就是圆的直径,从而可以分别利用圆和正方形的面积公式表示出它们的面积,即可求得正方形面积是圆面积的几分之几;
解答:解:如图所示,
(1)在正方形里面画一个最大的圆,设正方形的边长为a,
 ,
,
因为正方形的面积=a×a=a2,
圆的面积=π(
)2=
,
所以圆的面积÷正方形的面积=
÷a2=
;
(2)在圆里面画一个最大的正方形,设圆的半径是R,
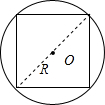 ,
,
因为圆的面积=πR2,
正方形的面积=2R×R÷2×2=2R2,
所以正方形的面积÷圆的面积=2R2÷πR2=
;
故答案为:
,
.
(1)在正方形里面画一个最大的圆,设正方形的边长为a,
 ,
,因为正方形的面积=a×a=a2,
圆的面积=π(
| a |
| 2 |
| πa2 |
| 4 |
所以圆的面积÷正方形的面积=
| πa2 |
| 4 |
| π |
| 4 |
(2)在圆里面画一个最大的正方形,设圆的半径是R,
 ,
,因为圆的面积=πR2,
正方形的面积=2R×R÷2×2=2R2,
所以正方形的面积÷圆的面积=2R2÷πR2=
| 2 |
| π |
故答案为:
| π |
| 4 |
| 2 |
| π |
点评:解答此题的关键是:依据画图弄清楚圆的半径与正方形的边长的关系,进而表示出各自的面积,求得面积之间的关系.

练习册系列答案
相关题目