Question

一个平行四边形的底与一个长方形的长相等，且它们的周长也相等，那么它们的面积

1. A.
   一样大
2. B.
   平行四边形大
3. C.
   长方形大

Answer 1

C
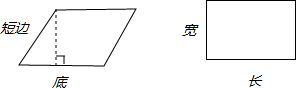
分析：因为平行四边形的面积=底×高，长方形的面积=长×宽；由“一个平行四边形的底与一个长方形的长相等，且它们的周长也相等”可知：只要知道长方形的宽与平行四边形的高的大小关系，即可比较面积大小，又因长方形的宽与平行四边形的短边相等，则长方形的宽大于平行四边形的高，所以长方形的面积大．
解答：如图所示，长=底，宽=短边，高＜短边，
则长方形的面积＞平行四边形的面积；
；
故答案为：C．
点评：解答此题的关键是：利用作图及二者的周长相等，比较出长方形的宽与平行四边形的高的大小关系，即可比较面积大小．