Question

作线段AB和CD，且AB和CD互相垂直平分，交点为O，AB=2CD．分别取OA、OB、OC、OD的中点A′、B′、C′、D′，连结CA′、DA′、CB′、DB′、AC′、AD′、BC′、BD′得到一个四角星图案．将此四角星沿水平方向向右平移2厘米，作出平移前后的图形．

Answer 1

分析：根据垂直平分线的意义，画线段AB（4厘米），作AB的垂直平分线段CD（2厘米）交AB于点O，再分别取OA、OB、OC、OD的中点A′、B′、C′、D′，连结CA′、DA′、CB′、DB′、AC′、AD′、BC′、BD′得到一个四角形图案A′B′C′D′；再根据平移图形的特征，把四角形图案A′B′C′D′的四个顶点分别向右平移2厘米，再首尾连结各点，即可得到四角形图案A′B′C′D′向右平移2厘米后的图形A″B″C″D″．

解答：解：根据题意作图如下：
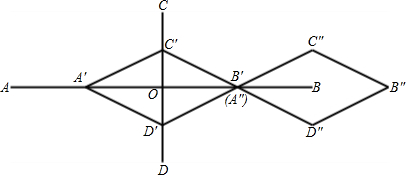
故答案为：

点评：本题主要是考查垂直平分线段的特征、作平移后的图形．平移的规律（性质）：经过平移，对应点所连的线段平行且相等，对应线段平行且相等、对应角相等．注意：平移后，原图形与平移后的图形全等．