Question

【题目】若.

(1)求证:；

(2)令,写出的值,观察并归纳出这个数列的通项公式；

(3)证明:存在不等于零的常数，使是等比数列,并求出公比的值.

Answer 1

【答案】(1)证明见解析；（2）an=；（3）.

【解析】试题分析：(1)假设，可得，与相矛盾，进而可得；(2) 写出的值，分别观察分子、分母与之间的关系，找出各项共同规律，可得；（3）根据待定系数法，由==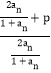,结合=·,可求得.

试题解析：(1)(采用反证法)若an+1=an,即=an,解得an=0,1.

从而an=an-1=……=a1=0,1,与题设a1>0,a1≠1相矛盾,

故an+1≠an成立.

(2)a1=,a2=,a3=,a4=,a5=,an=.

(3)因为==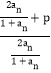,又因为=·q,

所以(2+p-2q)an+p(1-2q)=0,

因为上式是关于变量an的恒等式,故可解得q=,p=-1.