题目内容
用16个棱长1厘米的小正方体摆成不同形状的长方体,体积和表面积有什么变化?(画一画)
分析:16个棱长1厘米的正方体摆成形状不同的长方体,不管怎么拼组,拼成的长方体的体积不变,都等于这16个小正方体的体积之和,又因为16=1×16=2×8=4×4=2×2×4,一共有4种不同的摆法,由此先确定拼组后的长方体的长宽高,再分别计算出它们的表面积即可解决问题.
解答:解:如图,16个小正方体一共有4种不同拼组方法:
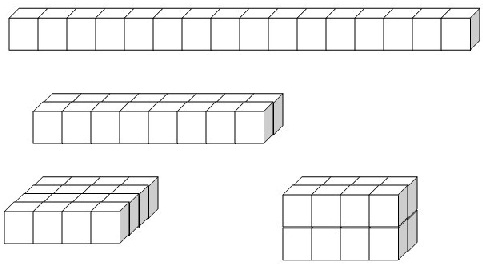
第一种拼成的长方体的表面积是:16×1×4+1×1×2,
=64+2,
=66(平方厘米),
第二种拼成的长方体的表面积是:(8×2+8×1+2×1)×2,
=(16+8+2)×2,
=26×2,
=52(平方厘米),
第三种拼成的长方体的表面积是:4×4×2+4×1×4,
=32+16,
=48(平方厘米),
第四种拼成的长方体的表面积是:4×2×4+2×2×2,
=32+8,
=40(平方厘米),
答:16个小正方体拼成长方体一共有4种不同的拼组方法,拼成的大长方体的体积不变,表面积各不相同.

第一种拼成的长方体的表面积是:16×1×4+1×1×2,
=64+2,
=66(平方厘米),
第二种拼成的长方体的表面积是:(8×2+8×1+2×1)×2,
=(16+8+2)×2,
=26×2,
=52(平方厘米),
第三种拼成的长方体的表面积是:4×4×2+4×1×4,
=32+16,
=48(平方厘米),
第四种拼成的长方体的表面积是:4×2×4+2×2×2,
=32+8,
=40(平方厘米),
答:16个小正方体拼成长方体一共有4种不同的拼组方法,拼成的大长方体的体积不变,表面积各不相同.
点评:此题考查了长方体的表面积公式的计算方法,抓住小正方体拼组长方体的方法,得出不同的拼组方法是解决本题的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目