Question

20．正方形边长为4．求阴影部分的面积．

Answer 1

分析 连接AC，由扇形公式先求出扇形ABC的面积，然后再求出直角三角形ABC的面积，然后相减即可得到阴影部分面积的$\frac{1}{4}$，然后再乘以4，但重复计算了中间重叠部分的面积，然后减去中间部分的面积即可．中间部分的计算方法为：用4个$\frac{1}{4}$圆的面积减去两个正方形的面积，然后除以2即可．

解答 解：连接AC，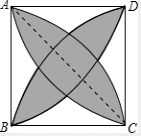

因为扇形ABC的面积=$\frac{1}{4}$π×16=4π，三角形ABC的面积=$\frac{1}{2}$×4×4=8，
所以$\frac{1}{4}$阴影部分的面积=4π-8，
因为4×（4π-8）=16π-32，
所以中间部分的面积=$\frac{1}{2}$（4×4π-2×4×4）=8π-16，
所以阴影部分的面积=16π-32-8π+16
=8π-16
=8×3.14-16
=25.12-16
=9.12

点评 此题考查了扇形的面积公式，解题的关键是：会计算中间重叠部分的面积，难道较大，要明确用2个$\frac{1}{4}$圆的面积减去正方形的面积是椭圆的面积，进行两次运算，结果中间重复减了，所以除以2，即是计算中间重叠部分的面积．