题目内容
【题目】如图是两条互相垂直的直线，相交于O点．
（1） 以O点为圆心，画一个半径为1cm的圆；
（2） 在圆内画一个最大的正方形，剩下的部分涂色表示；
（3）计算涂色部分的面积．
【答案】（1）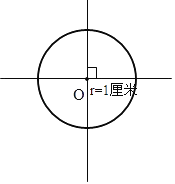
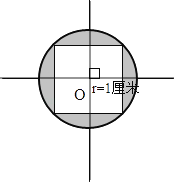
（2）
（3）1.14平方厘米
【解析】
（1）因为半径为1厘米，用圆规有针的一脚在O点，两脚叉开的大小为1厘米，然后旋转一周即可；
（2）在圆上画一个最大的正方形，该正方形的对角线是该圆的直径，据此即可画出这个正方形，剩余的部分涂色即可．
（3）0根据该正方形的对角线是该圆的直径，因此正方形的面积是底为圆的直径，高为半径的2个三角形的面积，据此可以计算出正方形的面积，再依据圆面积公式求得圆的面积，然后用圆的面积减去正方形的面积即是阴影部分的面积此题考查了画圆的方法以及在圆内作一个最大的正方形，明确最大正方形的对角线是圆的直径是解决问题的关键．
S阴=S圆﹣S正
=πr2﹣ 
dr×2
=3.14×12﹣ ×2×1×2
=3.14﹣2
=1.14（平方厘米）
答：这个阴影部分的面积是1.14平方厘米
练习册系列答案
相关题目
