题目内容
【题目】图中，平行四边形的面积是分成3个三角形，图中甲、乙、丙三个三角形的面积比是 ．
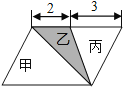
【答案】5：2：3．
【解析】
试题分析：由图知：平行四边形的面积是分成3个三角形，图中三个三角形的高都相等，都是平行四边形的高，设为h，甲的底是平行四边形的边，即乙和丙的底的和，根据三角形的面积公式是：底×高÷2，能分别表示出甲、乙、丙3个三角形的面积，从而算出它们面积的比．
解：因为甲、乙、丙三个三角形的高相等，即平行四边形的高，设为h，
又因为甲的底是平行四边形的边，即乙和丙的底的和：2+3=5，
所以甲的面积=5h÷2=
h，
乙的面积=2h÷2=h，
丙的面积=3h÷2=
h，
所以：甲：乙：丙=
：h：
=5：2：3．
答；甲、乙、丙三个三角形的面积比是 5：2：3．
故答案填5：2：3．
练习册系列答案
相关题目
