题目内容
 (2009?大竹县)如图,正方形ABCD中,边长为12cm,CE=2BE,AF=2BF,AE、CF交于点O,求阴影部分的面积.
(2009?大竹县)如图,正方形ABCD中,边长为12cm,CE=2BE,AF=2BF,AE、CF交于点O,求阴影部分的面积.分析: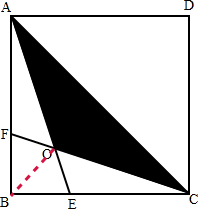 正方形ABCD中,边长为12cm,CE=2BE,AF=2BF,不难看出三角形AFO的面积=三角形BEO的面积;三角形BOF的面积=三角形BOE的面积,根据高一定时,三角形的面积与底成正比例的性质可得:三角形BOE的面积=
正方形ABCD中,边长为12cm,CE=2BE,AF=2BF,不难看出三角形AFO的面积=三角形BEO的面积;三角形BOF的面积=三角形BOE的面积,根据高一定时,三角形的面积与底成正比例的性质可得:三角形BOE的面积=
三角形EOC的面积,所以可得:三角形BOE的面积=
三角形BFC的面积,由此只要求出三角形BFC的面积即可求出空白处四个小三角形的面积,则阴影部分的面积就等于正方形的面积的一半-四个空白处小三角形的面积.
 正方形ABCD中,边长为12cm,CE=2BE,AF=2BF,不难看出三角形AFO的面积=三角形BEO的面积;三角形BOF的面积=三角形BOE的面积,根据高一定时,三角形的面积与底成正比例的性质可得:三角形BOE的面积=
正方形ABCD中,边长为12cm,CE=2BE,AF=2BF,不难看出三角形AFO的面积=三角形BEO的面积;三角形BOF的面积=三角形BOE的面积,根据高一定时,三角形的面积与底成正比例的性质可得:三角形BOE的面积=| 1 |
| 2 |
| 1 |
| 4 |
解答:解:正方形ABCD中,CE=2BE,AF=2BF,不难得出:
三角形AFO的面积=三角形BEO的面积;三角形BOF的面积=三角形BOE的面积,
因为BE:EC=1:2,
所以三角形EOC的面积=三角形BOE的面积的2倍;
则三角形BOE的面积=
三角形BFC的面积,
因为BF=12÷3=4(厘米),
所以三角形BFC的面积是12×4÷2=24(平方厘米),
则三角形BOF的面积=三角形BOE的面积=
×24=6(平方厘米),
三角形AFO的面积=三角形BEO的面积=6×2=12(平方厘米),
所以阴影部分的面积是:12×12÷2-12×2-6×2=72-24-12=36(平方厘米);
答:阴影部分的面积是36平方厘米.
三角形AFO的面积=三角形BEO的面积;三角形BOF的面积=三角形BOE的面积,
因为BE:EC=1:2,
所以三角形EOC的面积=三角形BOE的面积的2倍;
则三角形BOE的面积=
| 1 |
| 4 |
因为BF=12÷3=4(厘米),
所以三角形BFC的面积是12×4÷2=24(平方厘米),
则三角形BOF的面积=三角形BOE的面积=
| 1 |
| 4 |
三角形AFO的面积=三角形BEO的面积=6×2=12(平方厘米),
所以阴影部分的面积是:12×12÷2-12×2-6×2=72-24-12=36(平方厘米);
答:阴影部分的面积是36平方厘米.
点评:解答此题的关键是画出辅助线,分别求出空白处四个小三角形的面积,再利用正方形的面积的一半减去它们的面积之和就是阴影部分的面积.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2009?大竹县)小明从家骑车经过博物馆到游乐园,全程需2小时,如果他以同样的速度从家骑车直接到游乐园,可以省多长时间?
(2009?大竹县)小明从家骑车经过博物馆到游乐园,全程需2小时,如果他以同样的速度从家骑车直接到游乐园,可以省多长时间?