题目内容
【题目】三角形内部有2008个点,将这2008个点与三角形的三个顶点连接,将三角形分割成互不重叠的三角形共( )个.
A.4017 B.2008 C.4016 D.6024
【答案】A
【解析】
因为此题点数较多,这就要求我们寻找规律,可以通过画图来寻找规律:
通过画图发现,当点数为1时,三角形的个数为3;当点数为2时,三角形的个数为5;当点数为3时,三角形的个数为7,…,当点数为n时,三角形的个数为2n+1.
画图如下:

(1)图①中,当△ABC内只有1个点时,可分割成3个互不重叠的小三角形.
(2)图②中,当△ABC内只有2个点时,可分割成5个互不重叠的小三角形.
(3)图③中,当△ABC内只有3个点时,可分割成7个互不重叠的小三角形.
(4)根据以上规律,当△ABC内有n(n为正整数)个点时,可以把△ABC分割成(2n+1)个互不重叠的三角形.
因此三角形内部有2008个点,将三角形分割成互不重叠的三角形个数为:2n+1=2×2008+1=4017(个).
故选:A.

练习册系列答案
相关题目
【题目】下面是两种不同型号的电视机,2012年以来的销售情况统计表。(单位:万台)
年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
A型 | 35 | 38 | 32 | 30 | 25 |
B型 | 14 | 20 | 30 | 35 | 38 |
(1)完成统计图。
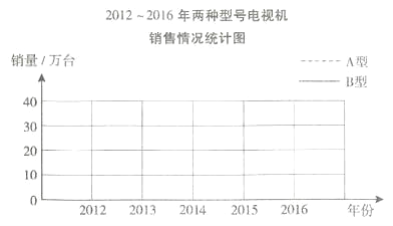
(2)A型产品________年至________年销售量下降最大,下降了________万台。
(3)B型产品________年至________年销售量上升最大,上升了________万台。
(4)如果你是商场经理,从上面统计图中能得到哪些信息?这些信息对你有什么帮助?