题目内容
组长给甲、乙两名青工各一箱零件的加工任务.每箱零件数相同.甲、乙两人刚开始的加工效率之比为5:4,他们同时开始工作,当他们加工的零件总数刚好是一箱的零件数目时,甲的效率降低20%,乙的效率提高20%,这样当甲加工完自己的一箱零件时,乙还剩有10个未加工完,则所加工的一箱零件有多少个?
解:提高工作效率后两人的工作效率的比是:
(5×80%):(4×120%)=4:4.8=5:6
设一箱x个,两人刚好做完一箱时,甲余(1- )x个,乙余(1-
)x个,乙余(1- )x-10个,
)x-10个,
5:6=(1- )x:[(1-
)x:[(1- )x-10],
)x-10],
5:6= x:[
x:[ x-10],
x-10],
[ x-10]×5=
x-10]×5= x×6
x×6
 x-50=
x-50=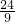 x,
x,
x=450
答:一箱零件有450个.
分析:开始的时候甲乙的工作效率之比为5:4,因此相同时间内甲乙所加工的零件数之比也为5:4,因此当加工的零件总数达到一箱时,甲加工的零件为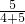 箱,,而乙加工了
箱,,而乙加工了 箱.随后甲的工作效率下降20%,也就是说甲的工作效率变为了原来的(1-20%)=80%;乙的工作效率提高20%,也就是说乙的工作效率变为了原来的(1+20%)=120%.因此此时甲乙两人的工作效率之比为(5×80%):(4×120%)=4:4.8=5:6.而这时甲还剩下1-
箱.随后甲的工作效率下降20%,也就是说甲的工作效率变为了原来的(1-20%)=80%;乙的工作效率提高20%,也就是说乙的工作效率变为了原来的(1+20%)=120%.因此此时甲乙两人的工作效率之比为(5×80%):(4×120%)=4:4.8=5:6.而这时甲还剩下1- 箱,甲乙两人此时的工作效率之比一定,据此可列方程解答.
箱,甲乙两人此时的工作效率之比一定,据此可列方程解答.
点评:本题的关键是根据工作效率的比一定,来列方程解答.
(5×80%):(4×120%)=4:4.8=5:6
设一箱x个,两人刚好做完一箱时,甲余(1-
 )x个,乙余(1-
)x个,乙余(1- )x-10个,
)x-10个,5:6=(1-
 )x:[(1-
)x:[(1- )x-10],
)x-10],5:6=
 x:[
x:[ x-10],
x-10],[
 x-10]×5=
x-10]×5= x×6
x×6 x-50=
x-50=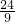 x,
x,x=450
答:一箱零件有450个.
分析:开始的时候甲乙的工作效率之比为5:4,因此相同时间内甲乙所加工的零件数之比也为5:4,因此当加工的零件总数达到一箱时,甲加工的零件为
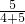 箱,,而乙加工了
箱,,而乙加工了 箱.随后甲的工作效率下降20%,也就是说甲的工作效率变为了原来的(1-20%)=80%;乙的工作效率提高20%,也就是说乙的工作效率变为了原来的(1+20%)=120%.因此此时甲乙两人的工作效率之比为(5×80%):(4×120%)=4:4.8=5:6.而这时甲还剩下1-
箱.随后甲的工作效率下降20%,也就是说甲的工作效率变为了原来的(1-20%)=80%;乙的工作效率提高20%,也就是说乙的工作效率变为了原来的(1+20%)=120%.因此此时甲乙两人的工作效率之比为(5×80%):(4×120%)=4:4.8=5:6.而这时甲还剩下1- 箱,甲乙两人此时的工作效率之比一定,据此可列方程解答.
箱,甲乙两人此时的工作效率之比一定,据此可列方程解答.点评:本题的关键是根据工作效率的比一定,来列方程解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目