题目内容
一条步行街上甲、乙两处相距600米,张华每小时走4千米,王伟每小时走5千米.8时整他们两人从甲、乙两处同时出发相向而行,1分钟后他们调头,反向而行,再过3分钟,他们又调头相向而行,依次按照1、3、5、7…(连续奇数)分钟调头行走.那么张华、王伟两人相遇时间是8时多少分?
解:4千米=4000米,5千米=5000米,1小时=60分,
张华的速度:4000÷60= (米/分钟);
(米/分钟);
王伟的速度:5000÷60= (米/分钟);
(米/分钟);
600÷(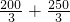 )
)
=600×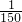 ,
,
=4(分钟);
也就是说两人保持相向4分既能相遇.
每次掉头分别用时 1 3 5 7 9 分钟,共25分钟,
相遇时用了25-1=24(分);
故在8点24分相遇.
答:张华、王伟两人相遇时间是8时24分.
分析:600m的距离相向而行要4分钟相遇,从第一次掉头后每掉头两次,等于相向而行两分钟,即在第五次掉头前一分钟相遇,
每次掉头分别用时1、3、5、7、9分钟,共25分钟,相遇时用了25-1=24分,由此推算出相遇的时刻.
点评:此题属于多次相遇问题,根据路程、速度、时间三者之间的关系灵活运用解决问题.
张华的速度:4000÷60=
 (米/分钟);
(米/分钟);王伟的速度:5000÷60=
 (米/分钟);
(米/分钟);600÷(
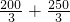 )
)=600×
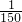 ,
,=4(分钟);
也就是说两人保持相向4分既能相遇.
每次掉头分别用时 1 3 5 7 9 分钟,共25分钟,
相遇时用了25-1=24(分);
故在8点24分相遇.
答:张华、王伟两人相遇时间是8时24分.
分析:600m的距离相向而行要4分钟相遇,从第一次掉头后每掉头两次,等于相向而行两分钟,即在第五次掉头前一分钟相遇,
每次掉头分别用时1、3、5、7、9分钟,共25分钟,相遇时用了25-1=24分,由此推算出相遇的时刻.
点评:此题属于多次相遇问题,根据路程、速度、时间三者之间的关系灵活运用解决问题.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目