题目内容
(1)甲地气温+10℃表示(________ ),乙地气温-2℃,(________ )地气温高.
(2)比较大小,用“>”“=”或“<”连接.-8________ 0 6.5________-6.5- ________-30
________-30
(3)平行四边形的面积一定,它的底和高成(________ )比例.
(4)如果a×8=b×5(a,b均不为0),那么a:b=(________ ):(________ ).
(5)一个三角形的周长是24厘米,三条边的长度比是5:4:3,其中最长的一条边是(________ )厘米.
(6)在一个比例中,两个外项互为倒数,其中一个内项是 ,另一个内项是(________ ).
,另一个内项是(________ ).
(7)甲数与乙数的比是5:9,乙数比甲数多(________ )%
(8)一个圆锥体的体积是9立方米,和它等底等高的圆柱体的体积是(________ )
(9)一个圆柱的底面半径是2厘米,高是2厘米,它的侧面展开图是一个(________ )形,这个圆柱的表面积是(________ )平方厘米.
(10)两个等底等高的圆柱和圆锥,它们的体积之和是24立方厘米,其中圆锥的体积是(________ )立方厘米.
(11)在一幅地图上,用20厘米长的线段表示实际距离100千米,这幅地图的比例尺是(________ ).
(12)把 :
: 化成最简整数比是(________ ),比值是(________ ).
化成最简整数比是(________ ),比值是(________ ).
(13)20米的80%是(________ )米,(________ )千克比60千克多20%
(14)一件工作,甲要4小时完成,乙要5小时完成,甲、乙工作时间之比是(________ ),工作效率之比是(________ ).
解:(1)甲地气温+10℃表示 零上10℃,乙地气温-2℃,甲地气温高;
(2)-8<0,6.5>-6.5- >-30;
>-30;
(3)平行四边形的面积一定,它的底和高成反比例;
(4)如果a×8=b×5(a,b均不为0),那么a:b=5:8;
(5)一个三角形的周长是24厘米,三条边的长度比是5:4:3,其中最长的一条边是10厘米;
(6)在一个比例中,两个外项互为倒数,其中一个内项是 ,另一个内项是
,另一个内项是 ;
;
(7)甲数与乙数的比是5:9,乙数比甲数多80%;
(8)一个圆锥体的体积是9立方米,和它等底等高的圆柱体的体积是27立方米;
(9)一个圆柱的底面半径是2厘米,高是2厘米,它的侧面展开图是一个长方形,这个圆柱的表面积是50.24平方厘米;
(10)两个等底等高的圆柱和圆锥,它们的体积之和是24立方厘米,其中圆锥的体积是6立方厘米;
(11)在一幅地图上,用20厘米长的线段表示实际距离100千米,这幅地图的比例尺是1:500000;
(12)把 :
: 化成最简整数比是8:5,比值是
化成最简整数比是8:5,比值是 ;
;
(13)20米的80%是16米,72千克比60千克多20%;
(14)一件工作,甲要4小时完成,乙要5小时完成,甲、乙工作时间之比是4:5,工作效率之比是5:4;
故答案为:零上10℃,甲,<,>,>,反,5,8,10, ,80,27立方米,长方,50.24,6,1:500000,8:5,
,80,27立方米,长方,50.24,6,1:500000,8:5, ,16,72,4:5,5:4.
,16,72,4:5,5:4.
分析:(1)、(2)根据在数轴上从左到右的方向就是数从小到大的顺序,正数大于0和一切负数,0大于一切负数解答.
(3)平行四边形的面积=底×高,面积一定,就是底与高的积一定,根据反比例的意义,底和高成反比例.
(4)根据比例的基本性质即可解答.
(5)根据按比例分配解答,把这个三角形的周长分成5+4+3=12(份),其中最长的边点 ,就是求24厘米的
,就是求24厘米的 是多少.
是多少.
(6)根据互为倒数性质,其积是1,再根据比例的基本性质,两外项之积等于两内项之积,一内项是 ,即可求出另一内项.
,即可求出另一内项.
(7)把甲数看作单位“1”,甲数与乙数的比是5:9,把甲数看作是5,乙数看作是9,用5与9的差除以甲数5即可.
(8)根据等底待高的圆柱的体积是圆锥的3倍解答.
(9)圆柱的侧面展开图形是一个长方形,其长、宽分别是圆柱的底面周长和高,由底面半径,根据圆周长=2πr可求出圆柱的底面周长,又由圆面积=πr2可求出圆柱两底的面积,进而求出圆柱的表面积.
(10)等底待高的圆柱的体积是圆锥的3倍,把圆锥的体积看作1,则圆柱的就是3,用和24除以它们的分率和即可求出圆锥的体积.
(11)根据比例尺的意义,即可求出此比例尺,注意单位统一,把100千米化成厘米主.
(12)根据比的基本性质,比的前、后项都乘3和6的最小公倍数6即可对此比进行化简;再根据比值的意义,用比的前项除以后项即可求出.
(13)根据求一个数的百分之几是多少,用乘法计算可解答第一步;把60看作单位“1”,另一数是1+20%,就是求60的1+20%是多少,用乘法计算.
(14)由甲、乙的工作时间,根据比的意义可求出甲、乙工作时间之比;再根据工作时间与工作效率成反比即可求出工作效率之比.
点评:本题考查的知识点比较多,有:负数的意义及其应用、正、负数的大小比较、百分数应用题、简单的工程问题、按比例分配应用题、求比值和化简比、比例的意义和性质、成正、反比例量的辩识、圆柱体的展开图、圆柱与圆锥体积的关系、比例尺等.
(2)-8<0,6.5>-6.5-
 >-30;
>-30;(3)平行四边形的面积一定,它的底和高成反比例;
(4)如果a×8=b×5(a,b均不为0),那么a:b=5:8;
(5)一个三角形的周长是24厘米,三条边的长度比是5:4:3,其中最长的一条边是10厘米;
(6)在一个比例中,两个外项互为倒数,其中一个内项是
 ,另一个内项是
,另一个内项是 ;
;(7)甲数与乙数的比是5:9,乙数比甲数多80%;
(8)一个圆锥体的体积是9立方米,和它等底等高的圆柱体的体积是27立方米;
(9)一个圆柱的底面半径是2厘米,高是2厘米,它的侧面展开图是一个长方形,这个圆柱的表面积是50.24平方厘米;
(10)两个等底等高的圆柱和圆锥,它们的体积之和是24立方厘米,其中圆锥的体积是6立方厘米;
(11)在一幅地图上,用20厘米长的线段表示实际距离100千米,这幅地图的比例尺是1:500000;
(12)把
 :
: 化成最简整数比是8:5,比值是
化成最简整数比是8:5,比值是 ;
;(13)20米的80%是16米,72千克比60千克多20%;
(14)一件工作,甲要4小时完成,乙要5小时完成,甲、乙工作时间之比是4:5,工作效率之比是5:4;
故答案为:零上10℃,甲,<,>,>,反,5,8,10,
 ,80,27立方米,长方,50.24,6,1:500000,8:5,
,80,27立方米,长方,50.24,6,1:500000,8:5, ,16,72,4:5,5:4.
,16,72,4:5,5:4.分析:(1)、(2)根据在数轴上从左到右的方向就是数从小到大的顺序,正数大于0和一切负数,0大于一切负数解答.
(3)平行四边形的面积=底×高,面积一定,就是底与高的积一定,根据反比例的意义,底和高成反比例.
(4)根据比例的基本性质即可解答.
(5)根据按比例分配解答,把这个三角形的周长分成5+4+3=12(份),其中最长的边点
 ,就是求24厘米的
,就是求24厘米的 是多少.
是多少.(6)根据互为倒数性质,其积是1,再根据比例的基本性质,两外项之积等于两内项之积,一内项是
 ,即可求出另一内项.
,即可求出另一内项.(7)把甲数看作单位“1”,甲数与乙数的比是5:9,把甲数看作是5,乙数看作是9,用5与9的差除以甲数5即可.
(8)根据等底待高的圆柱的体积是圆锥的3倍解答.
(9)圆柱的侧面展开图形是一个长方形,其长、宽分别是圆柱的底面周长和高,由底面半径,根据圆周长=2πr可求出圆柱的底面周长,又由圆面积=πr2可求出圆柱两底的面积,进而求出圆柱的表面积.
(10)等底待高的圆柱的体积是圆锥的3倍,把圆锥的体积看作1,则圆柱的就是3,用和24除以它们的分率和即可求出圆锥的体积.
(11)根据比例尺的意义,即可求出此比例尺,注意单位统一,把100千米化成厘米主.
(12)根据比的基本性质,比的前、后项都乘3和6的最小公倍数6即可对此比进行化简;再根据比值的意义,用比的前项除以后项即可求出.
(13)根据求一个数的百分之几是多少,用乘法计算可解答第一步;把60看作单位“1”,另一数是1+20%,就是求60的1+20%是多少,用乘法计算.
(14)由甲、乙的工作时间,根据比的意义可求出甲、乙工作时间之比;再根据工作时间与工作效率成反比即可求出工作效率之比.
点评:本题考查的知识点比较多,有:负数的意义及其应用、正、负数的大小比较、百分数应用题、简单的工程问题、按比例分配应用题、求比值和化简比、比例的意义和性质、成正、反比例量的辩识、圆柱体的展开图、圆柱与圆锥体积的关系、比例尺等.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
下面是甲乙两地2010年月平均气温情况统计表.
| 月 份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 甲地气温℃ | 4 | 8 | 13 | 16 | 20 | 24 | 27 | 28 | 24 | 20 | 15 | 8 |
| 乙地气温℃ | -10 | -8 | 4 | 15 | 23 | 30 | 35 | 34 | 36 | 19 | 12 | 4 |
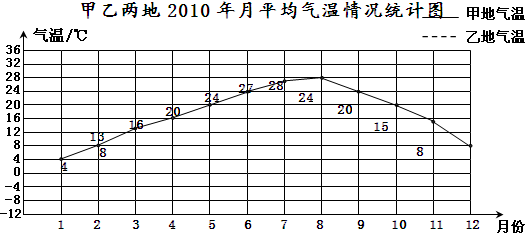
(1)根据统计表中的数据把上面的复式折线统计图补充完整.
(2)如果让你在甲、乙两地中选择一个地方居住,你会选择哪里?为什么?