题目内容
20.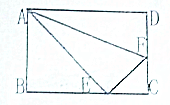 长方形ABCD,AD长9厘米,AB长6厘米,△ABE,△ADF,四边形AECF的面积相等,问:△AEF的面积是多少?
长方形ABCD,AD长9厘米,AB长6厘米,△ABE,△ADF,四边形AECF的面积相等,问:△AEF的面积是多少?
分析 由题意可知:△ABE、△ADF、四边形AECF的面积都等于长方形的面积的$\frac{1}{3}$,据此再用长方形的长和宽表示出三角形FCE的面积,进而解决问题.
解答 解:假设长方形的长和宽分别为9和6,
则长方形的面积为:9×6=54(平方厘米),
△ABE、△ADF、四边形AECF的面积都等于$\frac{1}{3}$×54=18(平方厘米),
则BE为:$\frac{1}{3}$×54×2÷6=6(厘米),所以CE为:9-6=3(厘米),
同理,DF为:$\frac{1}{3}$×54×2÷9=4(厘米),所以CF为:6-4=2(厘米),
因此三角形FCE的面积为3×2÷2=3(平方厘米),
三角形AEF的面积为:18-3=15(平方厘米).
答:△AEF的面积是15平方厘米.
点评 此题主要考查三角形和长方形的面积的计算方法的灵活应用,利用等量代换的方法即可求解.

练习册系列答案
相关题目