Question

三角形的周长是46厘米，其内有一点p到三条边的距离都是4厘米，这个三角形的面积是________平方厘米．

Answer 1

92
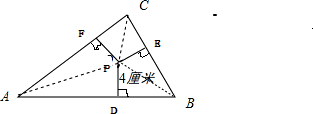
分析：如下图所示，三角形ABC的周长是46厘米，即：AB+BC+AC=46厘米；其内有一点p到三条边的距离都是4厘米，那么，过P作三边的垂线PF、PD、PE，则PF=PD=FE=4厘米，连接PA、PB、PC，得到三个三角形△PAC、△PAB、△PBC，它们的面积分别是s△PAC=AC×PF、S△PAB=AB×PD、S△PBC=BC×PE；三个小三角形的面积之和就等于这个大三角形的面积．由此得解．
解答：如图，

S△ABC=S△PAC+S△PAB+S△PBC=AC×PF+AB×PD+BC×PE，
因为PF=PD=FE=4厘米，代入上式，得：
S△ABC=×4×（AC+AB+BC），
=2×46，
=92（平方厘米）；
答：这个三角形的面积是 92平方厘米；
故答案为：92．
点评：此题的关键是连接PA、PB、PC，把三角形分作3个小三角形，小三角形的高相等，在求面积时，刚好提取出高来，余下的部分又刚好是三角形的周长，由此得解．