题目内容
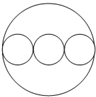图中外大圆的周长等于三个内圆周长的和．
正确
分析：根据圆的周长公式可知大圆周长为πd；三个小圆周长之和为：πd′+πd″+πd″′，由于d=d′+d″+d″′；结合乘法分配律即可求解．
解答：大圆的直径为d，三个小圆的直径依次为d′，d″，d″′；
则大圆周长为：πd；
三个小圆周长之和为：πd′+πd″+πd″′=π（d′+d″+d″′）；
因为d=d′+d″+d″′，
所以三个小圆周长之和与大圆周长比较，一样长．
故答案为：√．
点评：考查了圆的周长之间的大小比较，本题关键是乘法分配律的运用．
分析：根据圆的周长公式可知大圆周长为πd；三个小圆周长之和为：πd′+πd″+πd″′，由于d=d′+d″+d″′；结合乘法分配律即可求解．
解答：大圆的直径为d，三个小圆的直径依次为d′，d″，d″′；
则大圆周长为：πd；
三个小圆周长之和为：πd′+πd″+πd″′=π（d′+d″+d″′）；
因为d=d′+d″+d″′，
所以三个小圆周长之和与大圆周长比较，一样长．
故答案为：√．
点评：考查了圆的周长之间的大小比较，本题关键是乘法分配律的运用．
练习册系列答案
阅读快车系列答案
相关题目
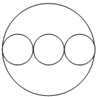图中外大圆的周长等于三个内圆周长的和．