题目内容
用不同的方法求如图所示图形的面积


考点:组合图形的面积
专题:平面图形的认识与计算
分析:(1)添加如下图所示的两种辅助线,这个图形的面积等于图中长方形的面积加上挺行的面积,代入公式计算即可解答.
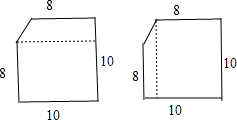
(2)添加如下图所示的三种辅助线,这个图形的面积等于图中两个长方形的面积之和或两个长方形的面积之差,据此根据图形确定它们的长与宽的值,代入公式计算即可解答.
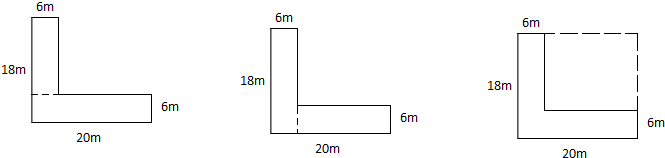

(2)添加如下图所示的三种辅助线,这个图形的面积等于图中两个长方形的面积之和或两个长方形的面积之差,据此根据图形确定它们的长与宽的值,代入公式计算即可解答.

解答:
解:(1)方法一:(8+10)×(10-8)÷2+8×10
=18+80
=98(平方米)
方法二:(8+10)×(10-8)÷2+8×10
=18+80
=98(平方米)
答:如图所示图形的面积是98平方米.
(2)方法一:(18-6)×6+20×6
=12×6+20×6
=72+120
=192(平方米)
方法二:18×6+(20-6)×6
=18×6+14×6
=32×6
=192(平方米)
方法三:18×20-(18-6)×(20-6)
=360-12×14
=360-168
=192(平方米)
答:这个图形的面积是192平方米.
=18+80
=98(平方米)
方法二:(8+10)×(10-8)÷2+8×10
=18+80
=98(平方米)
答:如图所示图形的面积是98平方米.
(2)方法一:(18-6)×6+20×6
=12×6+20×6
=72+120
=192(平方米)
方法二:18×6+(20-6)×6
=18×6+14×6
=32×6
=192(平方米)
方法三:18×20-(18-6)×(20-6)
=360-12×14
=360-168
=192(平方米)
答:这个图形的面积是192平方米.
点评:此题考查组合图形的面积的计算方法,一般都是转化到规则图形中,利用面积公式计算解答.

练习册系列答案
相关题目
