Question

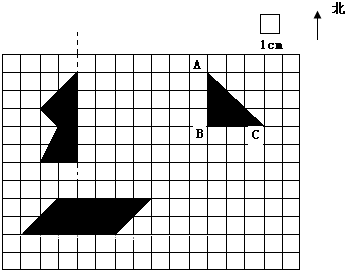
在下面的点子图中完成如下操作：
①画出轴对称图形的另一半；
②先观察：三角形ABC中，点A在点C的________偏________°处．再画出三角形ABC绕点C顺时针旋转90°后的图形．
③用一条直线把平行四边形分成两部分，使它们的面积比是2：3．
④已知一个图形的是这个图形是什么样的？请在点子图中选择合适的位置把它画出来．

Answer 1

西    北45
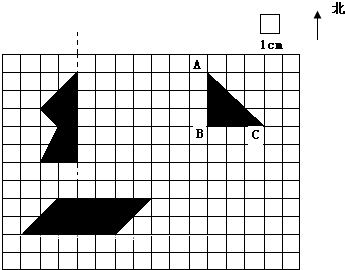
分析：（1）根据轴对称图形的性质，沿一条直线对折后，直线两旁的部分能够完全重合，由此即可画出图形的另一半，使它成为一个轴对称图形．
（2）由图意可知，此三角形是一个等腰直角三角形，再据图上的方向标，即可得出两点的方向关系；根据图形旋转的方法，先把与点C相连的线段，绕点C顺时针旋转90°后，再根据线段与三角形的位置关系，把三角形画出来，即可得出旋转后的图形．
（3）因为平行四边形的面积=底×高，若两个平行四边形的高相等，则其面积比就等于对应底的比；所以将平行四边形的底边按2：3分开，然后过分点A作这条底边的临边的平行线，即可完成解答．
（4）本题要运用到图形的平均分，并且表示出是这一个图形的，这里要会图形的操作．
解答：（1）因为对应点的连线被这条对称轴垂直平分，所以先描出关于这条直线的对应点，再把它们依次连接起来即可得出这个轴对称图形；
（2）三角形ABC中，点A在点C的西偏倍45°处；先把与点C相连的线段，绕点C顺时针旋转90°后，再根据线段与三角形的位置关系，把三角形画出来，即可得出旋转后的图形，如图所示；
（3）将平行四边形的底边按2：3分开，然后过分点A作这条底边的临边的平行线，所得到的两部分的面积比即为2：3，如图所示；
（4）如图所示，即为原图形：
；
故答案为：西、北45．
点评：（1）此题考查了轴对称图形的性质和画轴对称图形的方法．
（2）此题考查了图形的旋转方法的灵活应用．
（3）此题主要考查平行四边形的面积公式的灵活应用．
（4）本题主要考查了对平均分的理解，及图形平均分的操作．