题目内容
把圆柱的底面平均分成若干等份,切开后,拼成一个长方体,这个长方体与圆柱相比( )
分析:设圆柱的半径为r,高为h;根据圆柱的切割方法与拼组特点可知:拼成的长方体的长是圆柱底面周长的一半,即是πr;宽是半径的长度是r,高是原来圆柱的高h,由此利用长方体的表面积公式,代入数据即可解答.
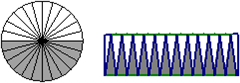

解答:解:设圆柱的半径为r,高为h;则拼成的长方体的长πr;宽是r,高是h,
(1)原来圆柱的表面积为:2πr2+2πrh;
拼成的长方体的表面积为:(πr×r+πr×h+h×r)×2=2πr2+2πrh+2hr;
所以拼成的长方体的表面积比原来的圆柱的表面积变大了;
(2)原来圆柱的体积为:πr2h;
拼成的长方体的体积为:πr×r×h=πr2h,
所以拼成的长方体和圆柱的体积大小没变.
所以拼成的长方体的表面积比原来的圆柱的表面积变大了,但是体积没变.
故选:B.
(1)原来圆柱的表面积为:2πr2+2πrh;
拼成的长方体的表面积为:(πr×r+πr×h+h×r)×2=2πr2+2πrh+2hr;
所以拼成的长方体的表面积比原来的圆柱的表面积变大了;
(2)原来圆柱的体积为:πr2h;
拼成的长方体的体积为:πr×r×h=πr2h,
所以拼成的长方体和圆柱的体积大小没变.
所以拼成的长方体的表面积比原来的圆柱的表面积变大了,但是体积没变.
故选:B.
点评:根据圆柱切割后拼组长方体的特点,得出这个长方体的长宽高是解决此类问题的关键.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
 把圆柱的底面平均分成16份切开后,照图拼成近似的长方体,( )发生了变化.
把圆柱的底面平均分成16份切开后,照图拼成近似的长方体,( )发生了变化.