Question

【题目】如图，正方形所在平面与四边形所在平面互相垂直， 是等腰直角三角形， ， ， .

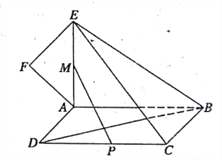
（1）求证： 平面；

（2）设线段的中点分别为，求异面直线与所成角的正弦值；

（3）求二面角的大小.

Answer 1

【答案】(1)见解析(2) （3） 45°

【解析】试题分析：

（1）要证明线面垂直，就要证线线垂直，由面面垂直的性质定理可得BC⊥平面ABEF，从而有AB⊥EF．又由平几知识得EF⊥EB，从而可得线面垂直，也即得面面垂直；

（2）求异面直线所成的角，一般要作出这个角，为此取BE中点N，可证MN与PC平行且相等，从而得平行四边形，有PM与CN平行，因此只要在中求出的正弦值即可；

（3）求二面角E－BC－D，就要找到它的平面角，由（1）的证明知∠EBA就是所要作的平面角，这个角是45°，因此二面角为45°．

试题解析：

（1）因为平面ABEF⊥平面ABCD，BC平面ABCD，BC⊥AB，

平面ABEF∩平面ABCD=AB，所以BC⊥平面ABEF．所以BC⊥EF．

因为△ABE为等腰直角三角形，AB=AE，

所以∠AEB=45°又因为∠AEF=45°，

所以∠FEB=45°+45°=90°，即EF⊥BE．

因为BC平面BCE，BE平面BCE，BC∩BE=B，所以EF⊥平面BCE．

（2）取BE的中点N，连结CN，MN，

则且，

所以PMNC为平行四边形，所以PM∥CN．

所以∠NCB为PM与BC所成角（或其补角）

正方形ABCD所在平面与四边形ABEF所在平面互相垂直，△ABE是等腰直角三角形，AB=AE，设AE=a，BN= ．BC=a，所以NC= ，在直角三角形NBC中， ．

（3）由（1）知BC⊥平面ABEF．所以BC⊥AB, BC⊥EB, 因此，∠EBA为二面角E﹣BC﹣D的平面角．又因△ABE是等腰直角三角形，所以∠EBA=45°

故二面角E﹣BC﹣D的大小为45°．