题目内容
聚星小学选派乒乓球队员参加市级小学生乒乓球比赛,打算从5名队员中选出2名队员,一共有 种不同的选法.
考点:握手问题,排列组合
专题:传统应用题专题
分析:由于每个人都可以和另外的4个人组合,一共有:5×4=20(种)组合;又因为两个人只有一种组合方式,去掉重复计算的情况,实际只有:20÷2=10(种)组合,然后据此列举即可.
解答:
解:(5-1)×5÷2
=20÷2
=10(种)
答:一共有10种不同的选法.
故答案为:10.
=20÷2
=10(种)
答:一共有10种不同的选法.
故答案为:10.
点评:本题看作握手问题的实际应用,要注意去掉重复计算的情况,如果数量比较少可以用枚举法解答,注意要按顺序写出,防止遗漏.如果数量比较多可以用公式:握手次数=n(n-1)÷2解答.

练习册系列答案
相关题目



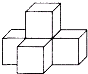 一个立体图形如图所示.
一个立体图形如图所示.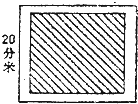 如图,一块正方形毛毯,要想在它的四围绣上花边,你能算出花边的长是多少分米吗?
如图,一块正方形毛毯,要想在它的四围绣上花边,你能算出花边的长是多少分米吗?