题目内容
9．已知平行四边形ABCD的高AH=HC=4cm，阴影面积Ⅱ与I相等，求平行四边形的面积．
分析 如图：已知阴影面积Ⅱ与I相等，所以△ABC=ACD（两个三角形等底等高），则S1=S2，根据扇形面积公式求出扇形的面积，用扇形面积减去阴影部分I的面积即可求出S1的面积，然后用两个阴影部分的面积加上两个空白部分的面积就是平行四边形的面积．据此解答．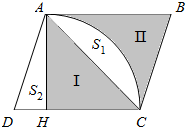
解答 解：已知阴影面积Ⅱ与I相等，所以△ABC=ACD（两个三角形等底等高），则S1=S2，
S扇形：3.14×42×$\frac{1}{4}$
=3.14×$16×\frac{1}{4}$
=12.56（平方厘米），
阴影I的面积：4×4÷2=8（平方厘米），
S1空白：12.56-8=4.56（平方厘米），
，所以平行四边形ABCD的面积是：4.56×2+8×2
=9.12+16
=25.12（平方厘米），
答：平行四边形的面积25.12平方厘米．
点评 此题考查的目的是理解掌握三角形的面积公式、扇形的面积公式及应用，关键是利用等量代换的方法求出空白部分S1=S2．
练习册系列答案
名牌学校分层周周测系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
19．脱式计算．
| 300+200×4 | 213×2-317 | （710+190）×6 |
| 1-$\frac{4}{9}$+$\frac{2}{9}$ | $\frac{5}{8}$+$\frac{3}{8}$-$\frac{1}{4}$ | 48÷6×205 |
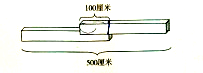将两根一样长的木条部分重叠钉在一起形成一根新木条，新木条长500厘米，中间重叠部分长100厘米，这两根木条各长多少厘米？
