题目内容
【题目】已知函数![]() ,设关于
,设关于![]() 的方程
的方程![]() 有
有![]() 个不同的实数解,则
个不同的实数解,则![]() 的所有可能的值为( )
的所有可能的值为( )
A. 3 B. 1或3 C. 4或6 D. 3或4或6
【答案】B
【解析】由已知, ![]() ,令
,令![]() ,解得
,解得![]() 或
或![]() ,则函数
,则函数![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减,极大值
上单调递减,极大值![]() ,最小值
,最小值![]() .
.
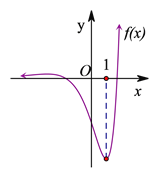
综上可考查方程![]() 的根的情况如下(附函数
的根的情况如下(附函数![]() 图):
图):
(1)当![]() 或
或![]() 时,有唯一实根;
时,有唯一实根;
(2)当![]() 时,有三个实根;
时,有三个实根;
(3)当![]() 或
或![]() 时,有两个实根;
时,有两个实根;
(4)当![]() 时,无实根.
时,无实根.
令![]() ,则由
,则由![]() ,得
,得 ,
,
当![]() 时,由
时,由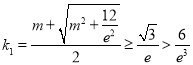 ,
,
符号情况(1),此时原方程有1个根,
由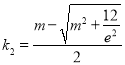 ,而
,而![]() ,符号情况(3),此时原方程有2个根,综上得共有3个根;
,符号情况(3),此时原方程有2个根,综上得共有3个根;
当![]() 时,由
时,由![]() ,又
,又![]() ,
,
符号情况(1)或(2),此时原方程有1个或三个根,
由![]() ,又
,又![]() ,符号情况(3),此时原方程有两个根,
,符号情况(3),此时原方程有两个根,
综上得共1个或3个根.
综上所述, ![]() 的值为1或3.故选B.
的值为1或3.故选B.

练习册系列答案
相关题目