题目内容
1．最少用3个等边三角形可以拼成一个等腰梯形，最少用2个等边三角形可以拼成一个平行四边形．分析 （1）因梯形是只有一组对边平行的四边形，用2个完全一样的等边三角形能拼成一个平行四边形，要使另一组对边不平行，就要再在平行的一组对边上，再加上一个完全相等的等边三角形．据此解答；
（2）两个完全一样的三角形可以拼成一个平行四边形，等边三角形是特殊的三角形，所以两个完全一样的等边三角形可以拼成一个平行四边形．
解答 解：（1）根据分析可知．至少用3个等边三角形才能拼成一个等腰梯形．
如下图：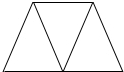
（2）用2个完全一样等边三角形可以拼成一个平行四边形：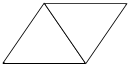
故答案为：3，2．
点评 本题的关键是根据梯形和平行四边形的特征求出最少需要的等边三角形的个数．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
11．下面各题中，商大于1的是（ ）
| A． | 5.04÷6 | B． | 76.5÷45 | C． | 45÷50 | D． | 0.84÷2.8 |
一张长8厘米，宽4厘米的长方形纸，从下边的中点和右上角顶点连线一条线段，沿这条线段剪去一个角（如图），剩下的面积是多少？
9．轻松口算．
| 1.5×0.3= | 0.36+0.64= | 0.96÷0.3= | 17.2×2= |
| 9-3.6= | 1÷0.625= | 3.6+35.7+6.4= | 19.6÷2÷5= |
6．下面四个式子中，结果与“472-5.2-4.8”相等的是（ ）
| A． | 472-5.2+4.8 | B． | 472+5.2+4.8 | C． | 472-（5.2-4.8） | D． | 472-（5.2+4.8） |