Question

【题目】将指定的数填入下表中，要求每个格子里一个数字，表中的每横行从左到右数字由小到大，每竖列从上到下数字也由小到大．

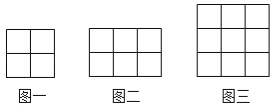
（1）将1﹣4的自然数填入表①中，共有多少种方法？

（2）将1﹣6的自然数填入表②中，共有多少种方法？

（3）将1﹣9的自然数填入表③中，共有多少种方法．

Answer 1

【答案】（1）2种；（2）5种；（3）21种

【解析】

试题分析：（1）要符合每横行从左到右数字由小到大，每竖列从上到下数字也由小到大排列．图一中，1只能在A的位置，4只能在D的位置，2和3可在B、C这两个格子中排列，所以共有2种方法；

（2）图二中，1只能在A的位置，6只能在F的位置，2只能在B和D，5只能在C、E的位置，数字5在C，有2种排列，数字5在E，又有3种排列方法；所以一共有2+3=5（种）．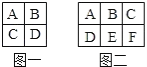

（3）由（2）的规律已经知道，6格是5种，1、2、3确定后，剩下的6个一定是5种；由此进行求解．

解答：解：（1）如图，1和4是固定的，另外两格随便选，2种．

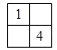
如下：

；

（2）1和6是固定的，其余的不确定：

（3）由（2）的规律已经知道，6格是5种；

1、2、3确定后，剩下的6个一定是5种，比如：

同理：

也对各对应5个；

但是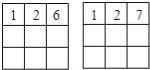例外，对应的不是5个．因为第一排右边的数限制了下面的数．

如下：

所以：共计5+5+5+4+2=21（种）

同理，以上所有情况倒过来后都有一一对应的种类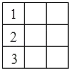

翻了一番，共21×2=42（种）．