题目内容
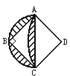
【题目】如图所示，正方形ABCD的面积为2平方厘米，它的对角线长AC=2厘米，扇形ACD是以D为圆心，以AD为半径的圆面积的一部分，那么阴影部分的面积是 平方厘米．
【答案】π﹣2
【解析】
试题分析：由图意可织：阴影部分的面积=半圆的面积﹣三角形ABC的面积+（S扇ACD﹣S△ACD），由正方形的面积是2平方厘米可求其边长，又因ABCD是正方形，AC=2厘米，将数据代入等式即可求得阴影部分的面积．
解：设正方形的边长为a，圆的半径=2÷2=1厘米，
则a2=2，
阴影部分的面积=半圆的面积﹣三角形ABC的面积+（S扇ACD﹣S△ACD），
=
π×12﹣a2+
π×a2﹣a2，
=
π﹣1+π﹣1，
=π﹣2（平方厘米）；
答：那么阴影部分的面积是π﹣2平方厘米．
故答案为：π﹣2．
练习册系列答案
相关题目
【题目】下面是冬冬家一、二、三月份的水、电、煤气费的统计表。
月份 | 水费/元 | 电费/元 | 煤气费/元 | 合计/元 |
一月 | 8.60 | 25.6 | 30.0 | |
二月 | 12.8 | 33.5 | 45.5 | |
三月 | 9.4 | 21.4 | 22.0 |
（1）分别算出每个月水、电、煤气的总费用，将上表填完整。
（2）哪个月费用最多？哪个月最少？相差多少元？
（2）三个月共交费多少元？