题目内容
10.先数一数,再填一填,你能发现什么规律?| 三角形个数 | 1 | 2 | 3 | 4 | 5 | 6 | … |
| 小棒根数 | 3 | 5 | … |
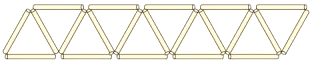
120个这样的三角形,需要多少根小棒?②有59根小棒,能摆出多少个这样的三角形?
分析 搭第一个图形需要3根火柴棒,结合图形,发现:后边每多一个图形,则多用2根火柴,由此推理得出一般规律即可解答问题.
解答 解:结合图形,发现:搭第n个图形,需要3+2(n-1)=2n+1(根).故填表如下:
| 三角形个数 | 1 | 2 | 3 | 4 | 5 | 6 | … |
| 小棒根数 | 3 | 5 | 7 | 9 | 11 | 13 | … |
需要小棒:120×2+1
=240+1
=241(根)
答:摆120个这样的三角形,需要241根小棒.
(2)当2n+1=59时
2n=58
n=29
答:59根小棒能摆29个三角形.
点评 此题考查了规律型中的图形变化问题,要能够从图形中发现规律:搭第n个图形,需要3+2(n-1)=2n+1(根).

练习册系列答案
相关题目
18.气象小组在一天的四个不同时间测得的气温记录.
(1)但有一块地方被墨水盖住了.你能知道20时的气温是多少℃吗?
(2)这一天的最高气温是多少摄氏度?最低气温是多少摄氏度?
(3)你还想到了哪些?
| 时间 | 2时 | 8时 | 14时 | 20时 | 平均 |
| 气温(℃) | 13 | 16 | 24 | 18 |
(2)这一天的最高气温是多少摄氏度?最低气温是多少摄氏度?
(3)你还想到了哪些?
2.3:10的前项加上6,如果要使比值不变,后项应该( )
| A. | 加上20 | B. | 加上6 | C. | 扩大2倍 |

 王爷爷靠墙围了一个羊圈.(如图)
王爷爷靠墙围了一个羊圈.(如图)