题目内容
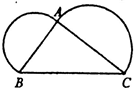 如图,以直角三角形ABC的两条直角边为直径作两个半圆,己知这两段半圆弧的长度之和是37.68厘米,那么三角形ABC的面积最大是
如图,以直角三角形ABC的两条直角边为直径作两个半圆,己知这两段半圆弧的长度之和是37.68厘米,那么三角形ABC的面积最大是72
72
平方厘米(π取3.14).分析:根据圆的周长公式C=πd,用AB与AC的长度表示出两段半圆弧的长度之和,由此得出AB+AC的和,而要使三角形ABC的面积最大,AB与AC最接近,由此确定AB与AC的长度,进而再根据三角形的面积公式S=ab÷2,即可求出三角形ABC的面积最大值.
解答:答:因为3.14×(AB+AC)÷2=37.68,
所以AB+AC=37.68×2÷3.14=24(厘米);
要使三角形ABC的面积最大,AB与AC最接近,
由此确定AB与AC的长度为:AB=AC=12(厘米),
所以三角形ABC的面积最大是:12×12÷2=72(平方厘米);
答:三角形ABC的面积最大是72平方厘米.
故答案为:72.
所以AB+AC=37.68×2÷3.14=24(厘米);
要使三角形ABC的面积最大,AB与AC最接近,
由此确定AB与AC的长度为:AB=AC=12(厘米),
所以三角形ABC的面积最大是:12×12÷2=72(平方厘米);
答:三角形ABC的面积最大是72平方厘米.
故答案为:72.
点评:解答此题的关键是知道当两个数的和一定时,两个数越接近,乘积就越大.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
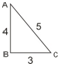 如图,将直角三角形ABC以AB为轴旋转一周,得到的圆锥体积是V,那么V=( )
如图,将直角三角形ABC以AB为轴旋转一周,得到的圆锥体积是V,那么V=( )| A、12π | B、36π | C、48π |
 如图,等腰直角三角形ABC的腰为10厘米;以A为圆心,EF为圆弧,组成扇形AEF;阴影部分甲与乙的面积相等.求扇形所在的圆面积.
如图,等腰直角三角形ABC的腰为10厘米;以A为圆心,EF为圆弧,组成扇形AEF;阴影部分甲与乙的面积相等.求扇形所在的圆面积. 如图是一个直角三角形,两条直角边的长分别为3cm、4cm,斜边的长为5cm.如果以斜边为轴旋转一周,求所形成的立体图形的体积算式是( )
如图是一个直角三角形,两条直角边的长分别为3cm、4cm,斜边的长为5cm.如果以斜边为轴旋转一周,求所形成的立体图形的体积算式是( )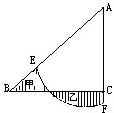 如图,等腰直角三角形ABC的腰为10厘米;以A为圆心,EF为圆弧,组成扇形AEF;阴影部分甲与乙的面积相等.求扇形所在的圆面积.
如图,等腰直角三角形ABC的腰为10厘米;以A为圆心,EF为圆弧,组成扇形AEF;阴影部分甲与乙的面积相等.求扇形所在的圆面积. 如图,将直角三角形ABC以AB为轴旋转一周,得到的圆锥体积是V,那么V=
如图,将直角三角形ABC以AB为轴旋转一周,得到的圆锥体积是V,那么V=