Question

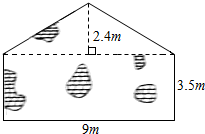
16．下图中涂色部分的面积占正方形面积的$\frac{8}{17}$，已知正方形的边长是17厘米．DE长多少厘米？

Answer 1

分析 正方形边长已知，根据正方形的面积公式“S=a²”可求得正方形的面积，已知涂色部分的面积占正方形面积的$\frac{8}{17}$，根据分数乘法的意义可求出涂色部分的面积，涂色部分是一直角三解形，直角边AD已知（正方形边长），根据三角形面积公式“S=$\frac{1}{2}$ah”，用三角形面积乘2除以AD的长度就是AE的长度．

解答 解：17²×$\frac{8}{17}$×2÷17
=289×$\frac{8}{17}$×2÷17
=272÷17
=16（厘米）
答：AD长16厘米．

点评 此题主要是考查正方形、三角形面积的计算，分数乘法的意义等，关键是三角形面积的灵活运用（三角形面积乘2除以高等于底，除以底等于高）．