Question

18．正方形的边长是24厘米，取两边中点与顶点连线，求阴影部分的面积．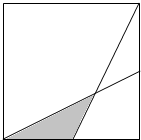

Answer 1

分析 过G点分别作CD和BD的平行线，交CD与点M，交BD与N，则三角形CGM的三角形CDE是相似三角形，GM：ED=CM：CD，又因E、F分别是BD、CD的中点，CE与BF交于G，所以四边形GMDE是正方形，GM=DM．据此解答．

解答 解：过G点分别作CD和BD的平行线，交CD与点M，交BD与N，则三角形CGM的三角形CDE是相似三角形，GM：ED=CM：CD，
又因E、F分别是BD、CD的中点，所以三角形CFG和三角形BEG是全等三角形，GE=GF，
三角形GFM和三角形GEN是全等三角形，所以GM=GN，四边形GMDE是正方形．
ED=24÷2=12（厘米）
CD=24（厘米）
CM=24-GM
   GM：ED=CM：CD，
   GM：12=（24-GM）：24
     24GM=12×24-12GM
24GM+12GM=288
     36GM=288
       GM=8
三角形CFG的面积
12×8÷2=48（平方厘米）
答：阴影部分的面积是48平方厘米．

点评 本题的关键是画辅助线，证明四边形GMDE是正方形，再根据相似三角形的知识求出GM的长是多少．