题目内容
【题目】已知函数![]() ,函数
,函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的表达式;
的表达式;
(2)若![]() ,函数
,函数![]() 在
在![]() 上的最小值是
上的最小值是![]() ,求
,求![]() 的值;
的值;
(3)在(2)的条件下,求直线![]() 与函数
与函数![]() 的图象所围成图形的面积.
的图象所围成图形的面积.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)讨论两种情况,求出![]() 结果相同,直接代入
结果相同,直接代入![]() ,即可得函数
,即可得函数![]() 的表达式;(2)利用基本不等式求得函数
的表达式;(2)利用基本不等式求得函数![]() 在
在![]() 上的最小值是
上的最小值是![]() 由
由![]() ,可得
,可得![]() 的值;(3)先求得直线
的值;(3)先求得直线![]() 与函数
与函数![]() 的图象的交点坐标,直线
的图象的交点坐标,直线![]() 与函数
与函数![]() 的图象所围成图形的面积就是
的图象所围成图形的面积就是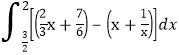 ,从而可得结果.
,从而可得结果.
试题解析:
(1)因为f(x)=ln|x|,所以当x>0时,f(x)=lnx,f′(x)=![]() ,
,
当x<0时,f(x)=ln(-x),f′(x)=![]() ·(-1)=
·(-1)=![]() .所以当x≠0时,函数y=g(x)=x+
.所以当x≠0时,函数y=g(x)=x+![]() .
.
(2)因为由(1)知当x>0时,g(x)=x+![]() ,
,
所以当a>0,x>0时,g(x)≥2![]() ,当且仅当x=
,当且仅当x=![]() 时取等号.所以函数y=g(x)在(0,+∞)上的最小值是2
时取等号.所以函数y=g(x)在(0,+∞)上的最小值是2![]() ,所以依题意得2
,所以依题意得2![]() =2,所以a=1.
=2,所以a=1.
(3)由 解得
解得 所以直线y=
所以直线y=![]() x+
x+![]() 与函数y=g(x)的图象所围成图形的面积S=
与函数y=g(x)的图象所围成图形的面积S=![]() dx=
dx=![]() +ln3-2ln2.
+ln3-2ln2.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案
相关题目
