Question

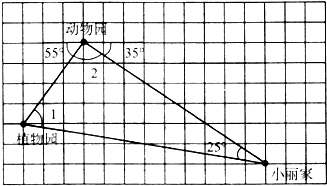
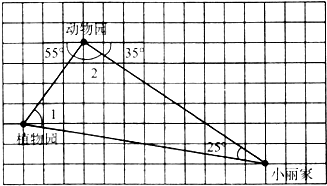（1）从图可看出，动物园、植物园、小丽家之间的连线组成了一个______角三角形．（2）∠1=______，∠2=______．
（3）动物园在小丽家的______面，植物园在动物园的______面．
（4）小丽准备乘出租车从家到动物园去，司机准备经植物园再到动物园，小丽会同意吗？为什么？

Answer 1

解：（1）∠2=180°-55°-35°=90°；
∠2是直角，所以这个三角形是直角三角形；

（2）∠2是90°，
∠1=180°-25°-90°=65°；

（3）动物园在小丽家的 西北面，植物园在动物园的 西南面．

（4）根据三角形任意两边的和大于第三边可知：
从家直接到动物园去，比经植物园再到动物园的路程短，所以不能经植物园再到动物园．
故答案为：直角，90°，65°，西北，西南．
分析：（1）（2）要确定三角形的类型，先求出最大角∠2的度数，由于55°、∠2和35°构成一个平角，根据平角是180°求出∠2的度数，进而判断三角形的类型；用三角形的内角和180°，减去25°，再减去∠2就是∠1的度数；
（3）根据“上北下南左西右东”进行求解；
（4）根据三角形三边的关系求解．
点评：本题综合考查了三角形的特性、内角和定理，以及确定方向方法的方法．