题目内容
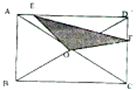如图，在长方形ABCD中，点O是长方形的中心，BC长20厘米，AB长12厘米，DE=4AE，CF=3DF，那么阴影部分的面积是多少平方厘米？
解：因为BC=20厘米，AB=12厘米，DE=4AE，CF=3DF，
所以可得：AE=4厘米，ED=16厘米，DF=3厘米，FC=9厘米，
所以阴影部分的面积为：S△ACD-S△AOE-S△OFC-S△EDF，
=0.5×12×20-0.5×4×6-0.5×9×10-0.5×16×3，
=120-12-45-24，
=39（平方厘米）；
答：阴影部分面积是39平方厘米．
分析：BC=20厘米，AB=12厘米，所以可得：AE=4厘米，ED=16厘米，DF=3厘米，FC=9厘米，
观察图形可知：阴影部分的面积等于长方形面积的一半减去图中涂色的三个三角形的面积；
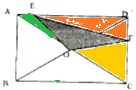
点评：此题主要考查了三角形面积公式的灵活应用，这里要注意组合图形的面积的转化方法．
所以可得：AE=4厘米，ED=16厘米，DF=3厘米，FC=9厘米，
所以阴影部分的面积为：S△ACD-S△AOE-S△OFC-S△EDF，
=0.5×12×20-0.5×4×6-0.5×9×10-0.5×16×3，
=120-12-45-24，
=39（平方厘米）；
答：阴影部分面积是39平方厘米．
分析：BC=20厘米，AB=12厘米，所以可得：AE=4厘米，ED=16厘米，DF=3厘米，FC=9厘米，
观察图形可知：阴影部分的面积等于长方形面积的一半减去图中涂色的三个三角形的面积；
点评：此题主要考查了三角形面积公式的灵活应用，这里要注意组合图形的面积的转化方法．
练习册系列答案
考前必练系列答案
相关题目
两个形状和大小都一样的直角三角形△ABC和△DEF，如图放置，它们的面积都是2003平方厘米，而每一个三角形的顶点恰好都落在另一个三角形的斜边上．这两个直角三角形的重叠部分是一个长方形，那么四边形ADEC的面积为
（2008?宝应县）（1）如表每小方格面积1平方厘米，先在图中画一个长4cm，宽3cm的长方形，再在长方形中画一个最大的圆，求出圆的面积．
（1）如表每小方格面积1平方厘米，先在图中画一个长4cm，宽3cm的长方形，再在长方形中画一个最大的圆，求出圆的面积．